February 2010 - Page 3 of 4 - Math and Multimedia

Introduction to the Concept of Area

February 12, 2010 GB Elementary School Geometry, Elementary School Mathematics

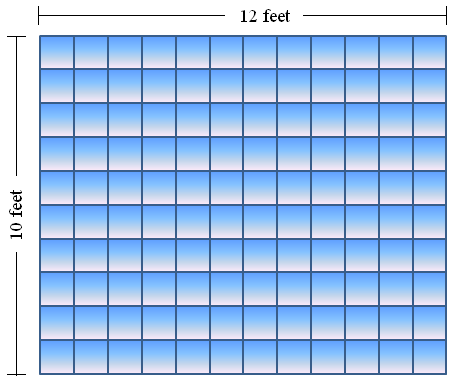
Suppose a room floor with length 12 feet and width 10 feet shown in Figure 2 is to be tiled using of a 1 foot by 1 foot tile shown in Figure 1, then it is clear 120 tiles are needed.

Figure 1 – A square representing a tile measuring 1 foot by 1 foot.

There are cases, of course, that some tiles have be to cut due to the size restriction of the room. For instance, How many 1 foot by 1 foot tile do we need to cut to cover a floor of a room measuring 10.5 by 12.5 feet? How many tiles are needed to cover the entire floor?

To explore more, click the here to open the GeoGebra applet and answer the questions following the applet.

Figure 2 – Tiles covering a room with length 12 ft and width 10 ft.

From the GeoGebra applet questions above, it is clear that the number of tiles that can cover an entire room is the product of its length and its width, whether the tiles are cut or not. The number of square feet (tiles in our problem) that covers the room is what we call its area. Therefore, we can think of area as the number of square units that entirely covers a bounded region – square units because we can always choose the units that we will use. For example, I can choose meter as unit instead of feet in the problem above.

Hence, we can say that the area of a room measuring 10 feet by 12 feet is 120 square feet. Generalizing, if we let L be the length of the rectangle and W its width and A its area, we can conclude that A = L x W.

If the length and the width of the rectangle are equal, then the rectangle is a square. If we let S be the side of the square, then A = S x S or A = S².

Of course, not all figures are rectangles or squares. There are curves and irregular figures. Don’t worry, we will discuss them in the future. This is just the start of the Area Tutorial Series.

9 comments area of a rectangle, area of a square, formula for area, GeoGebra

GeoGebra Tutorial 8 – Tracing the Graphs of Trigonometric Functions

February 10, 2010 GB GeoGebra, Software Tutorials

This is the eighth tutorial of the GeoGebra Intermediate Tutorial Series. If this is your first time to use GeoGebra, you might want to read the GeoGebra Essentials Series.

In this tutorial, we use the Input bar to create mathematical objects particularly a circle, an arc, and a point that traces the sine and cosine function. In doing the tutorial, we learn the following:

use the GeoGebra keyboard commands to construct various geometric objects
use the GeoGebra trace function
change the interval of the x-axis

Proof Tutorial 2: Proving Square Root of 2 is Irrational by Contradiction

February 8, 2010 GB College Mathematics, Number Theory, Problem Solving and Proofs

One of the most difficult proof strategies in mathematics is proof by contradiction. If P, for example, is a statement or a conjecture, one strategy to prove that P is true is to assume that P is not true and find a contradiction so that the statement not P does not hold. If not P does not hold, it follows that P is true.

One well-known proof that uses proof by contradiction is proof of the irrationality of $\sqrt{2}$ . If we consider P to be the statement “ $\sqrt{2}$ is irrational”, then not P is the opposite statement or “ $\sqrt{2}$ is rational”. To use proof by contradiction, we assume that $\sqrt{2}$ is rational, and find a contradiction somewhere. If this happens, then we would have shown that $\sqrt{2}$ is indeed irrational.

Before proceeding, recall that a rational number is a fraction with non-zero denominator. We know that all fractions can be expressed in lowest term. A fraction in $\displaystyle\frac{a}{b}$ is said to be in lowest term if $a$ and $b$ have no common divisors except $1$ .

On the other hand, irrational numbers cannot be expressed as fractions. They are decimal numbers that do not end and do not repeat. For example, $0.10100100010000...$ is an irrational number (the three dots means and so on which means that the number does not end). The most popular irrational number is $\pi$ .

Now, we prove our conjecture.

Conjecture: The $\sqrt{2}$ is irrational.

Proof:

Suppose $\sqrt{2}$ is rational, then it can be expressed in fraction form $\displaystyle\frac{a}{b}$ . Let us assume that our fraction is in lowest term, i.e., their only common divisor is $1$ . Then,

$\sqrt{2} = \displaystyle\frac{a}{b}$

Squaring both sides, we have

$2= \displaystyle\frac{a^2}{b^2}$

Multiplying both sides by $b^2$ yields

$2b^2= a^2$ *

Since $a^2 = 2b^2$ , we can conclude that $a^2$ is even because whatever the value of $b^2$ has to be multiplied by $2$ . If $a^2$ is even, then $a$ is also even. Since $a$ is even, no matter what the value of $a$ is, we can always find an integer that if we divide $a$ by $2$ , it is equal to that integer. If we let that integer be $k$ , then $\displaystyle\frac{a}{2} = k$ which means that $a = 2k$ .

Substituting the value of $2k$ to $a$ in *, we have $2b^2= (2k)^2$ which means that $2b^2=4k^2$ . Dividing both sides by $2$ , we have $b^2 = 2k^2$ . That means that the value $b^2$ is even, since whatever the value of $k$ you have to multiply it by $2$ . Again, if $b^2$ is even, then $b$ is even.

This implies that both $a$ and $b$ are even, which means that both the numerator and the denominator of our fraction are divisible by $2$ . This contradicts our assumption that $\displaystyle\frac{a}{b}$ has no common divisor except $1$ . Since we found a contradiction, our assumption is, therefore, false. Hence, the theorem is true.

Notice that I have highlighted the word suppose and assume in the proof. This is one unique feature of proof by contradiction. You can always assume, most of the time, the opposite of the conjecture as long as the following statements are logically valid.

Leave a comment indirect proof, irrational numbers, irrationality of square root of 2, methods of proof, Number Theory, proof by contradiction, proof strategies, proof tutorial, pure mathematics, rational numbers

« 1 2 3 4 »