Geometric Sequences and Series

June 9, 2010 GB Calculus and Analysis, College Mathematics, High School Algebra, High School Mathematics

Introduction

We have discussed about arithmetic sequences, its characteristics and its connection to linear functions. In this post, we will discuss another type of sequence.

The sequence of numbers 2, 6, 18, 54, 162, … is an example of an geometric sequence. The first term 2 is multiplied by 3 to get the second term, the second term is multiplied by 3 to get the third term, the third term is multiplied by 3 to get the fourth term, and so on. The same number that we multiplied to each term is called the common ratio. Expressing the sequence above in terms of the first term and the common ratio, we have 2, 2(3), 2(3²), 2(3³), …. Hence, a geometric sequence, also known as a geometric progression, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio.

The Sierpinski triangle below is an example of a geometric representation of a geometric sequence. The number of blue triangles, the number of white triangles, their areas, and their side lengths form different geometric sequences. It is left to the reader, as an exercise, to find the rules of these geometric sequences.

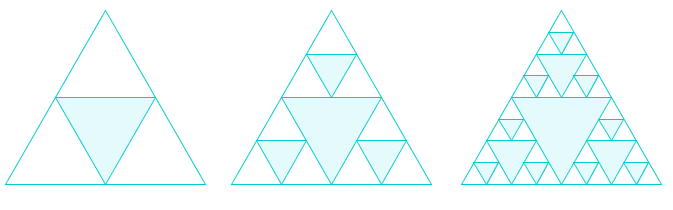
Figure 1 - The Seriepinski Triangles.

To generalize, if a₁ is its first term and the common ratio is r, then the general form of a geometric sequence is a₁, a₁r, a₁r², a₁r³,…, and the n^th term of the sequence is a₁r^n-1.

A geometric series, on the other hand, is the sum of the terms of a geometric sequence. Given a geometric sequence with terms a₁r, a₁r², a₁r³,…, the sum S_nof the geometric sequence with n terms is the geometric series a₁ + a₁r + a₁r², a₁r³ + … + ar^n-1. Multiplying S_n by -r and adding it to S_n, we have

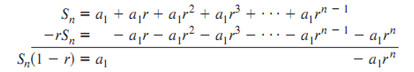
Hence, the sum of a geometric series with n terms, and $r \neq 1 = \displaystyle\frac{a_1(1-r^n)}{1-r}$ .

Sum of Infinite Geometric Series and a Little Bit of Calculus

Note: This portion is for those who have already taken elementary calculus.

The infinite geometric series $\{a_n\}$ is the the symbol $\sum_{n=1}^\infty a_n = a_1 + a_2 + a_3 + \cdots$ . From above, the sum of a finite geometric series with $n$ terms is $\displaystyle \sum_{k=1}^n \frac{a_1(1-r^n)}{1-r}$ . Hence, to get the sum of the infinite geometric series, we need to get the sum of $\displaystyle \sum_{n=1}^\infty \frac{a_1(1-r^n)}{1-r}$ . However, $\displaystyle \sum_{k=1}^\infty \frac{a_1(1-r^n)}{1-r} = \lim_{n\to \infty} \frac{a_1(1-r^n)}{1-r}$ .

Also, that if $|r| < 1$ , $r^n$ approaches $0$ (try $(\frac{2}{3})^n$ or any other proper fraction and increase the value of $n$ ), thus, $\displaystyle \sum_{n=1}^\infty \frac{a_1(1-r^n)}{1-r} = \lim_{n \to \infty} \frac{a_1(1-r^n)}{1-r} = \frac{a_1}{1-r}$ . Therefore, sum of the infinite series $\displaystyle a_1 + a_2r + a_2r^2 + \cdots = \frac{a_1}{1-r}$ .

One very common infinite series is $\displaystyle \sum_{n=1}^{\infty} \frac{1}{2n} = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \cdots$ , or the sum of the areas of the partitions of the square with side length 1 unit shown below. Using the formula above,

$\displaystyle \sum_{n=1}^{\infty} \frac{1}{2n} = \frac{a_1}{1-r} = \frac{\frac{1}{2}}{1-\frac{1}{2}} = 1$ .

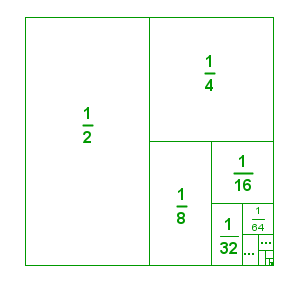
Figure 2 - A representation of an infinite geometric series.

This is evident in the diagram because the sum of all the partitions is equal to the area of a square. We say that the series $\displaystyle \sum_{n=1}^{\infty} \frac{1}{2n}$ converges to 1.

8 comments common ratio, geometric progressions, geometric sequence, infinite geometric sequence, sierpinski triangle, sum of infinite geometric series

Geometric Sequences and Series

Leave a ReplyCancel reply