The Binomial Expansion
Note: This is the second part of the Binomial Expansion Series
Part I: Milkshakes, Beads, and Pascal’s Triangle
Part II: Binomial Expansion
In the Milkshakes, Beads, and Pascal’s Triangle article, we have shown that the combination of the binary numbers 1 and 0 may be interpreted as the number the flavors of milk shakes, or the number of possible paths of the bead in our Galton board as shown in Table 1. Recall that in the Milkshake problem, Issa was given a choice to combine any number of flavors from four fruits: Apple, Banana, Chico and Durian. Thus, 0101 means banana-durian milkshake. On the other hand, in the beads problem, 0101 is LRLR or the bead went to the left after hitting the peg in row A, right in after hitting the peg in row B, left after hitting the peg in row C and right after hitting the peg in row D.
Figure 1 shows the possible combinations if there are only two and three rows of hexagonal pegs, or equivalently two or three fruits. Examine the tables and try to see if you can come up with a strategy on systematically creating tables for bigger number of rows/number of flavors.
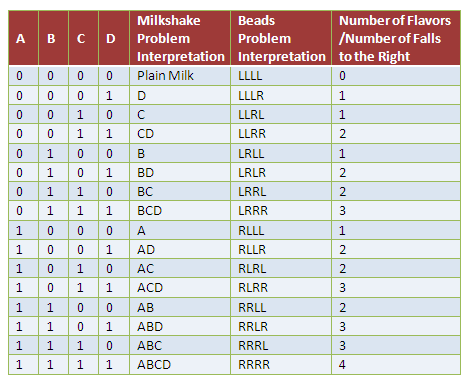
Table 1
We can see that if we have two flavors (or two rows of hexagonal pegs), there are 22 = 4 possible combinations; if we have three flavors (or three rows of hexagonal pegs), we have 23 = 8 possible combinations; and if we have four flavors (or four rows of hexagonal pegs) we have 24 = 16 possible combinations. We can therefore make a conjecture:
Conjecture: In the nth row of the Pascal’s triangle, there are 2n number of elements. That is
The tables in Figure 1 shows the possible arrangements of 1s and 0s in Pascal’s triangles with fewer rows, or fewer number of fruits.
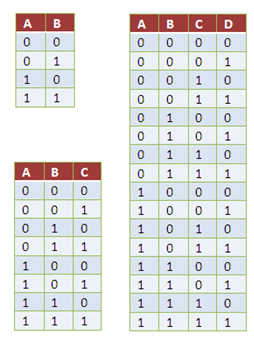
Figure 1
Replacing 0s with x’s and 1s with y’s, and getting the product of each row, we come up with the table in Figure 2. We can see that in the table, we have x2 + 2xy + y2, x3 + 3x2y + 3xy2 + y3 and x4 + 4x3y + 6x2y2 + 4xy3 + y4. As we can see, the coefficients of the binomial expansions are (1,2,1), (1,3,3,1) and (1,4,6,4,1) which are numbers in the Pascal’s triangle. We can also see that (x + y)2 = x2 + 2xy + y2, (x + y)3 = x3 + 3x2y + 3xy2 + y3 and (x+y)4 = x4 + 4x3y + 6x2y2 + 4xy3 + y4. Now it seems that the numbers in the Pascal’s triangle has something to do with the terms of the numerical coefficients of (x+y)n, where n is a positive integer.
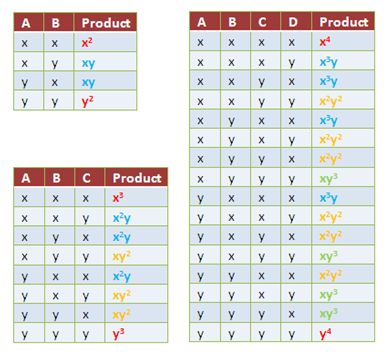
Figure 2
Using the combination notation to denote n objects taken k at a time, we have
.
Using the pattern, it follows that
Using the summation notation we have This equation is called, the binomial expansion. Note that this is just our conjecture. The proof of this equation requires knowledge of mathematical induction, which we will discuss in the future.