Is mathematics an exact science?
In many sciences, we conduct experiments many times and hypothesize or make conclusions. We can grow two groups of plants, place one group in a room with no sunlight, and place the other group outdoors. The plants inside a dim room die, and the plants in the garden live. We conclude that plants need sunlight.

But are we absolutely sure that our conclusion or hypothesis true? What about the plants under the caves that live despite the lack of sunlight? What about the plants under the sea?
These are the uncertainties that we encounter in most sciences. There many variables that should be considered, and our conclusion could sometimes be questioned.
On the other hand, in mathematics, no amount of experiment is enough to make a valid conclusion unless all possible cases are exhausted. However, in most math problems, it is impossible to exhaust all possible cases. Take, for example, the following conjecture:
The sum of two even integers is even.
Although, we cannot pair and add all even integers (there are infinitely many of them), we can argue that this conjecture is indeed true using logical and valid arguments. These arguments put together is called proof (see actual proof here).

Now, this is what is so special about mathematics. Most of the time, we are sure what we are talking about (Hmmm… are we really sure?).
We now ask the following questions:
Is the phrase “mathematics is an exact science” can be taken per se? Is the mathematics that we are studying nowadays that impregnable? Is mathematics consistent and free from contradictions?
The phrase mathematics is an exact science is really an ambiguous question. The term “exact” will vary in meaning. If you say that you can get exact answers from math questions, that is true sometimes.
True, mathematics is probably the most consistent among the sciences, but does it really live up to our expectations?
The truth is mathematics is NOT that mighty. In the following examples, I will discuss (forgive my amateurish attempt) why mathematics is not, to a certain degree, as exact as we think it is.
Numbers
We have learned that an irrational number is a decimal that is never repeating and never ending. From this definition, there is no way that we can know or write the exact value of an irrational number. No matter how many digits of an irrational number we write, it will always be an approximation of the actual value. That is why writing is incorrect. The correct notation should be
. The
symbol means approximately equal to.
Geometry
The second example is from the most famous mathematics book ever written — The Elements, by Euclid. Despite the fact that it was used as a Geometry Bible for hundreds of years, and it is always referred to until now, if we examine it closely, it is actually flawed.
All the geometry theorems when we were in high school that we rigorously proved (or probably memorized) are consequences of the five postulates or axioms. In an axiomatic system, all theorems can be derived from the postulates. If the postulates are incorrect, have a flaw, or at least in doubt to be correct, then we cannot claim that Euclidean geometry is free from contradictions.
The five postulates of Euclidean geometry are stated below. To facilitate the discussion, I have restated it in a more understandable manner.
A line maybe drawn from any point to any point.
A line may be extended to both sides indefinitely.
A circle may be drawn with any center and any radius length.
All right angles are equal.
Given a parallel line on the same plane and a transversal intersecting the two lines, the interior angles on the same side add up to 180 degrees.
Proposition 1 of Euclid’s Elements tells us how to draw an equilateral triangle using postulates 1 and 3. From postulate 1, we can draw a line (needless to say, Euclid means line segment) from any point to any point, so we draw line segment AB (see figure below). From postulate 3, we can draw circles with any center or any radius length so we draw a circle with center A passing through point B, and a circle with center B passing through point A.
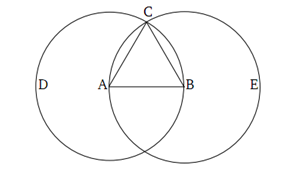
Although it is obvious that an equilateral triangle maybe created by connecting the two centers, and connecting the centers to one of the intersections (point C), there is no way that we can use the five postulates to conclude that the two circles actually intersect – don’t look at the drawing, just read the postulates. But that is supposed to be the structure of axiomatic systems: all the theorems/propositions should be derived from the postulates or theorems which are consequences of the postulates. In effect, the five postulates are not sufficient to show that the equilateral triangle exists. Therefore, the entire Euclidean geometry crumbles, if we were really to be very strict.
Calculus
Another example is the concept of limits. We say that the limit of 1/n as n approaches infinity is 0, but there is no exact number that can be substituted to n, such that 1/n is equal to 0. We can only choose a very large n to make 1/n as close to 0 as we please, but no matter how large n is, 1/n will never equal 0.
Now, after the discussion, try to answer the three questions raised above. As we can see, like Einstein said, everything is relative.
Existence Theorems
There are certain problems in mathematics where the only thing asked is the existence of a certain quantity, or in general, a mathematical object. During the time when transcendental numbers was only conjectured to exist, Georg Cantor, the pioneer of set theory, and one of my most admired mathematicians, proved that there are infinitely many of them without exhibiting one.
Conclusion
The effort to axiomatize geometry and other branches of mathematics only shows that mathematics is not a perfect science. Axiomatization is done not only to organize mathematics, but also to avoid contradiction. In fact, Kurt Godel proved that you cannot create an axiomatic system that is free from contradiction. The theorem is called Godel’s Incompleteness Theorem.
_______
Photo Credit: Corn Planted by Western Scrub Jays by Noel Zia Lee, Jedia Hamlet by Chris B urke