This is the fifth tutorial in the GeoGebra Essentials Series. If you are not familiar with GeoGebra, you may want to read the Introduction to GeoGebra post and prior tutorials. They contain the pre-requisites of this tutorial.
In the tutorial below, menu commands, located in the menu bar, are in brown bold text, and submenus are denoted by the > symbol. For example, Options>Labeling> New Points Only means, click the Options menu, choose Labeling from the list, then select New Points Only. The tool texts are colored orange. For example, New Point means the new point tool.
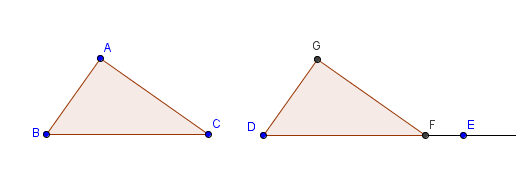
In this tutorial, we will mimic compass and straightedge construction using GeoGebra’s Compass tool, Segment and Ray tools. We use the concept of the SSS congruence1 to construct a triangle congruent to a given triangle.
In doing the tutorial, we are going to learn the following:
- Use the tools we have discussed in previous tutorials – Segment tool, Polygon tool
- Learn how to use new tools including Raytool and Compass tool.
|
1. Open GeoGebra. Select Geometry from the Perspective panel at the Sidebar on the right of the window. We want to automatically label all points so we can refer to them easily. To do this, select Options>Labeling> New Points Only from the menu bar. |
 |
2. To construct triangle ABC, select the Polygon tool and click three different locations on the Graphics view, then click point A to close the polygon.
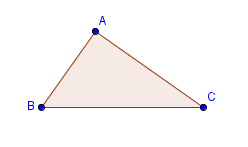 Figure 1 |
|
3. Our next task is to construct a triangle congruent to triangle ABC. We use the concept of congruence, SSS congruence1 in particular. We copy the length of the sides of the triangle and produce another triangle. First, we copy BC, but before we do that, we first construct a where we will place the side congruent to BC. |
 |
4. To construct ray DE, select the Ray through Two Points tool, then click two different locations on the Graphics view. Your drawing should look like Figure 2.
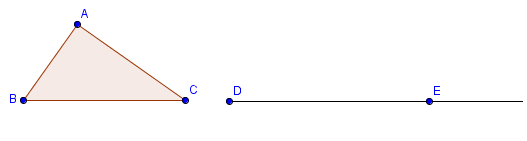 Figure 2 |
 |
5. Next, we use the Compass tool to measure the side lengths of BC and then use ray DE to construct a segment congruent to it. To copy the length of BC, select the Compass tool and click side BC (not the points but the segment). Note that as you move the mouse, a circle is formed with radius congruent to the length of BC. Click point D to construct the circle with center D and length BC. |
 |
6. We now determine the intersection of the circle and the ray. Select the Intersect tool, and then click their intersection to construct point F as shown below. Now, we know that BC is congruent to DF.
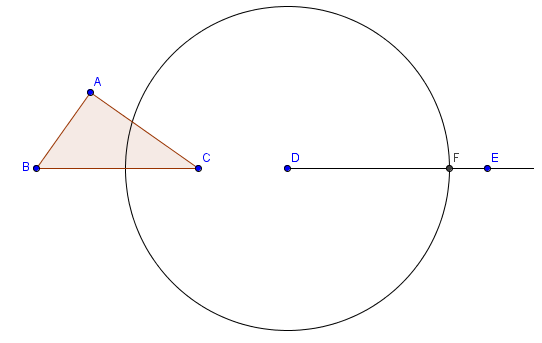 Figure 3 |
|
7. Next, we hide the circle. To do this, right click the circle and then click Show Object. |
 |
8. Now, we construct the segment congruent to AB. To do this select the Compass tool, select segment AB and then click on point D. |
 |
9. To construct the third side (the segment congruent to AC) select the Compass tool, select segment AC and then click on point F. |
 |
10. Use the Intersect tool to determine one of the intersections of the circles. We name this point G.
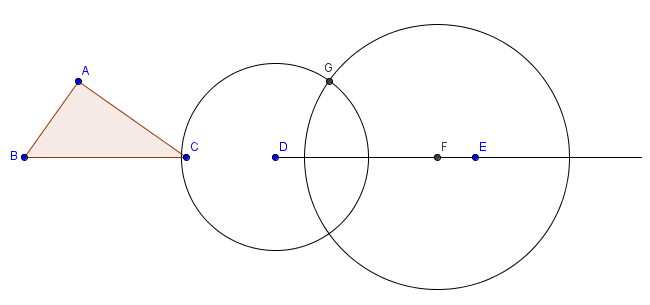 Figure 4 |
|
11. Now, hide the two circles by right clicking them and selecting Show Object from the context menu. |
 |
12. Using the Polygon tool, construct triangle DFG. |
|
13. Move the vertices of triangle ABC. What do you observe?2 |
|
14. Save your file by clicking File>Save on the menu bar. Name your file as essentials5. |
Notes:
1SSS congruence states that if the three corresponding sides of triangles are congruent, then the two triangles are congruent.
2Observe that if you move the vertices of triangle ABC, triangle GDF is always congruent to it. You can hide the ray and point A if you want.
Updated: 12 November 2015




