The Unfinished Game Problem
In the Milk, Beads and Pascal’s Triangle article, we have talked about the Sister’s Dilemma, and how they toss coins and later roll dice to solve their problem. In this post, we are going to talk more about tossing coins and how they are connected to other mathematical topics.
The Interrupted Game
In a chess tournament in your school, two of your classmates, Sherwin and Carlo, made it to the championship game. The championship game was a race to 6. The score was 5-3, in favor of Sherwin.
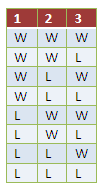
Figure 1
Suppose, Carlo got sick, and the school agreed to divide the prize money worth $500 based on the players’ chance of winning the championship, how should the money be divided fairly?
It is clear that Sherwin needs only one win to bag the prize, but Carlo needs to win three in a row — one loss, and the game is over for him. If we let W, be the Win of Carlo and L for his Loss, then Carlo needs a W-W-W in the three games. Any other combination, say, W-W-L or W-L-W loses the game.
Let us put all the possible combinations of Carlo’s three games with Sherwin in Table 1 where W means Carlo winning the game and L means Carlo losing the game. As we can see, there are 8 possible combinations, and the only chance of Carlo winning the championship is one; hence, the probability of Carlo winning is 1/8. Therefore, he should only get 1/8 of $500 or $62.50. The rest of the money (7/8 of 500 = 437.50) goes to Sherwin.
Tossing Three Coins
In the Gentle Introduction to Probability, Issa and Ishi, tossed a coin in making a decision which of them will go to their grandmother. In this post, we are going to toss more than one coin and see how is it connected to our previous problems in the combination series.
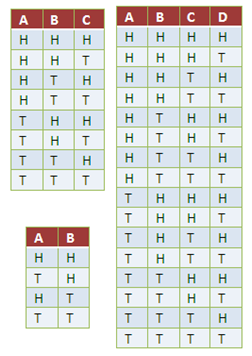
Figure 2
If we are going to toss a single coin, the possible outcomes are head (H) and tail (T). What about two coins. Well, we have HH, HT, TH and TT. In the figure above, we have the tables for the possible outcomes of 2 coins, 3 coins and 4 coins tossed.
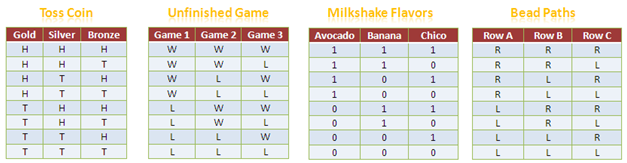
Figure 3
In Figure 3, we use gold, silver and bronze coins for better understanding. Notice that the table structure of the four tables are similar. We just have to replace the characters (letter or number) and the table is the exact duplicate. For instance, we can replace the W in the unfinished table 1 and L with 0, and our Unfinished Game table is the same as the milkshake table. Surprised?
Recall that in the milkshake flavor problem table, 1 means the flavor is present and 0 means the flavor is absent. Hence, 110 means the apple-banana milkshake and 000 is pure milkshake with no flavor. Note that they are also connected to the three tables.
The problem above shows that contrary to what many people believe, mathematics is an intertwined field, where some concepts surprisingly appear incognito in places where you expect them to be. The more you study it, the more you delve deeper, the more you see the connections between and among the concepts.