Operations on Integers – Addition
Introduction
The set of integers is composed of the negative integers, zero, and the positive integers. The integers can be visualized using the number line (see first figure), a horizontal line, where, by convention (agreed upon by mathematicians), the negative numbers are located at the left of zero, and the positive integers at the right of 0. In the number line, the number a is greater than the number b if a is at the right of b. Therefore, -2 is greater than -3, -1 is less than 1, 0 is greater than -4.
![]()
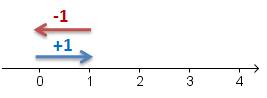
As shown in the figure above, each integer has a specific location (coordinate) on the number line. Aside from being a coordinate on the number line, each integer can also be considered as movement from 0. For example, +2 means moving 2 units to the right of 0, while -3 is moving 3 units to the left of 0.
Some elementary observations
One basic observation in looking at a particular integer as movement from zero is that if we move consecutively, say +2 and then +3, then we have moved 5 units to the right of 0. Therefore, we can think of the consecutive movements as addition. This implies that +4 + +8 are two consecutive movements – 4 units to the right, and after that, another 8 units to the right which gives us the sum +12.
The addition +5 + –4 are movements which 5 units to the right, and then 4 units to the left. This gives us +1. As we can observe, adding a negative integer b to a is also the same as subtracting b from a. That is, a + –b is the same as a – b.
We can also observe in the second figure that the addition +1 + –1 is are movements 1 unit to the right and then 1 unit to the left. This goes back to 0; therefore, +1 + –1 = 0. Of course, it is not difficult to see that +2 + –2 = 0,+3 + –3 = 0 and so on. In general, any number added to its negative is equal to 0 or a + –a = 0.
In adding two negative integers, the movements are to the left. For example, –5 + –6 is moving 5 units to the left, and then moving again 6 units to the left. That gives us -11. Since we have discussed that a – b = a + –b, –5 + –6 is the same as –5 – 6.
Another representation
Integers may be represented by colored chips. If we represent +1 with a blue chip and –1 with a red chip, in the previous example, moving to the right one unit and moving to the left 1 unit is equal to 0. Therefore, a pair of chips composed of both colors add up to 0; therefore, we can cancel them out as shown below.
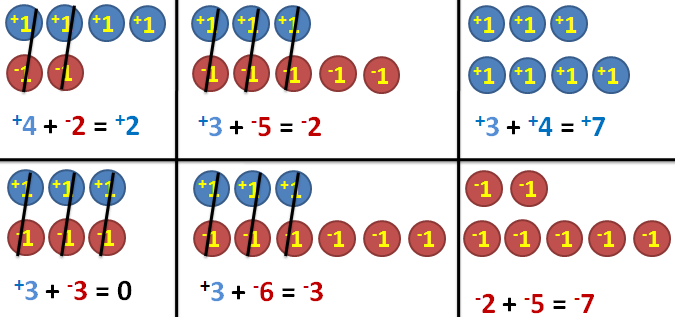
Looking at the addition in the third figure, you will probably observe that the sign (positive/negative) of the sum depends on the number of chips. Using these examples we can develop a strategy or generalization about adding integers.
For students who have not learned about integers yet, it is now your turn to think about them. After you have seen the pattern, answer the exercises below. See if you can answer them without using the chips representation.
Exercises:
- –8 + –3
- 5 + –13
- –21 + 4
- 8 + 4 + –15
- –21 + 23 + -19