Geometer’s Sketchpad Essentials 1 – Locating the Centroid

This is the first tutorial in the Geometer’s Sketchpad Essentials (GSP) Series.  In this tutorial, we are going to investigate the medians of a triangle. We will learn how to use the basic tools: Point Tool, Selection Arrow Tool, and the Segment Tool. If you are not familiar with GSP, you may want to read Introduction to Geometer’s Sketchpad.

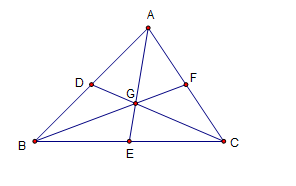
The output of our tutorial is shown in the Figure above; points D, E, and F are midpoints of the sides of triangle ABC. 

 Instructions

1.) Open Sketchpad.

2.) Select the Point tool and click three different locations on the drawing area or sketch pad.

3.) Select the Text tool and click all the points one by one to display their labels. Notice that GSP labels the points in alphabetical order.

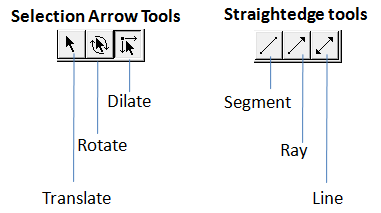
4.) Next, to construct segment AB, click the Segment tool (second figure), click point A and then click point B. The small arrow at the lower-right of the Segment tool indicates that there are other tools in that box. You can view these tools by clicking on that tool and holding the mouse button. The Segment tool is one of the tools in the Straightedge toolbox. The Selection Arrow tools are also shown in the figure below. 

5.) With the Segment tool still selected, construct segments BC and AC.

6.) To familiarize yourself with how dragging works in GSP, click the Selection tool (the Translate arrow) and drag the vertices, segments, and labels of the triangle. To drag the whole object, drag the across the entire construction to highlight all the objects, and then drag one of the objects. Now try the other two selection arrows and observe what happens. 

7.) To construct the midpoint, click segment AB (be sure that no point is selected), click the Construct menu from the Menu bar, and then click Midpoint.

8.) Now, to construct the midpoints of BC and AC, select both segments (again with no point selected), click the Construct menu, and then click Midpoints.

9.) Now, to label the midpoints, select the text Text tool and then click the midpoints of AB, BC, and AC in that order.

10.) Next, select the Segment tool, and then construct AE, BF and CD. These segments are the median of the triangle. A median of a triangle is a segment connecting the vertex to the midpoint of the opposite side.

11.) Use the Selection Arrow tool and move the vertices and segments of the triangle. What do you observe? Make a conjecture about your observation.

12.) Click File>Save,  and type centroid as the file name construction. We will need this construction in later tutorials.