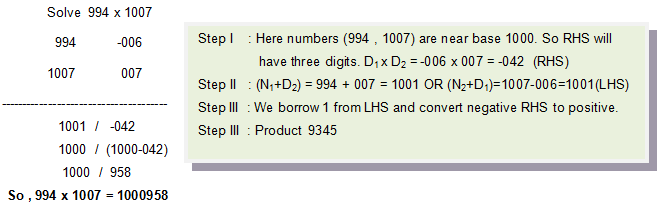
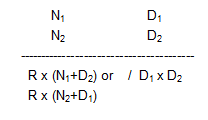Guest Post: Vedic Mathematics – Nikhilam Method of Multiplication Part 2

Sanjay Guilati (author) has been teaching computer and mathematics in Bhilai, state Chattisgarh in India for 15 years. Currently he is a  teacher in a senior secondary school and he is also involved in teacher training.  His online work can be found in Mathematics Academy.

In my previous post (download pdf here)  on multiplication by Nikhilam Method, I described how to multiply two numbers near base , when both are either above base or both are below base. Here we will discuss how to multiply two numbers out of which one is more and other is less than the base.

Example 1

Example 2

Let us now discuss how to multiply two numbers which are not near base (10 ,100 …..) . Product is found by  sub-sutra ‘Anurupyan’ meaning Proportionately. We will choose a proportionate sub-base.

A sub-base is the convenient multiplier or sub-multiplier of a base , e.g. 20, 30, 40 …… are the sub-bases of 10 which are respectively 2 , 3 , 4 times the base 10. Similarly 200 , 300 , …, 500 ,… etc are sub-bases of base 100.

The relation between sub-base and base is found by their division and is called a ratio. Thus sub-base : base is the ratio e.g. for sub-base 50 and base 10 , the ratio is 50 : 10 = 5:1 or 5. If sub-base is 50 but base is 100 then ratio becomes 50:100 i.e. 1:2 or 1/ 2.

The procedure followed here for multiplication is same as in previous lesson but with slight modification. The general points are as follows:

1. Choose the suitable base and sub-base by observing the numbers to be multiplied.
2. Two numbers to be multiplied are written one below the other. Their deviations from sub-base are written in front of the respective numbers.
3. Answer space is divided into LHS and RHS by a slash
4. RHS of the answer is the product of the deviations and shall have the number of digits equal to the number of zeroes in the base.
5. LHS of the answer is the sum of one number with the deviation of other and then multiplying by the ratio (sub-base : base)
6. Carry over of digit or digits from RHS to LHS , if any , is done only after getting complete  LHS of the answer (after multiplying by the ratio).
7. Slash is removed to get the answer.

Thus , if N₁ and N₂ are two numbers near the same sub-base , D₁ and D₂ are their deviations from their sub-bases , and R the ratio (sub-base : ratio) , then the product of N₁ and N₂ can be found as follows :