Understanding the Multiplication Principle

Amanda went shopping and bought three blouses (red, yellow, violet) and 2 skirts (blue,  green) as treat for herself for her birthday. The first thing she did when she got home was tried on the skirts and blouses. Question: In how many ways can she wear them?

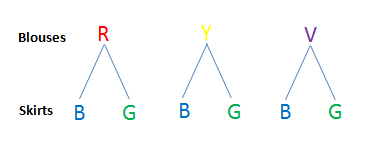
This problem can be easily answered by pairing each blouse to the two skirts. The red blouse can be paired with the blue or the green skirt. This is also similar to the yellow and violet blouses.

The pairing above can also be represented using a tree diagram as shown below. For each blouse, we can pair 2 skirts. Since there are three blouses, there are 3(2) = 6 possible ways to wear them.

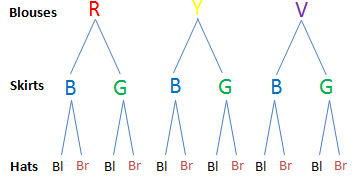
To Amanda’s surprise, here mother also bought her two hats — one brown, and one black.  In how many ways can Amanda wear the blouses, skirts, and hats?

This problem cannot be solved as easily as above.  But we do the same strategy: we use letter codes in ordered triples (blouses, skirts, hats). We arrange them using the first letter for their color as we have done above. R would stand for red, Y for yellow, and so on. Since we have three colors starting with B, we distinguish them from each other. We assign B for blue, Br for brown, and Bl for black.  Since all are in place, we form the ordered triples:

• (R,B, Br), (R,B, Bl), (R,G, Br), (R,G,Bl)
• (Y,B, Br), (Y,B, Bl), (Y,G, Br), (R,G,Bl)
• (V,B, Br), (V,B, Bl), (V,G, Br), (V,G,Bl)

By now, you would have realized that if we have m ways of doing something, and n ways of doing another thing, then there are mn ways of performing both actions.  This is called the multiplication principle or the rule of multiplication.

In effect, if we can travel from city A to B using a plane or a ship, and if can travel from city B to C using a plane or a bus, then there are 2 ways to do it from A to B and 2 ways to do it from B to C. Therefore, there are 4 ways of traveling from A to C via B. Those are plane-plane, plane-bus, ship-plane and ship-bus.