Squaring numbers always give a positive result or a 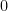 . For example,
. For example,  ,
,  ,
, 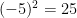 . Using this argument, it follows that we can always get the square root of
. Using this argument, it follows that we can always get the square root of 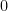 or any positive number. Now, what about the square root of a negative number, say,
or any positive number. Now, what about the square root of a negative number, say,  ?
?
Let’s see:  and
and 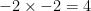 ; therefore, no number exists that when multiplied by itself equals
; therefore, no number exists that when multiplied by itself equals  . In fact, it looks like we cannot find the square root of any negative number.
. In fact, it looks like we cannot find the square root of any negative number.
Now, what if — just what if — we invent square root of negative numbers? Nobody would stop us right? We start with 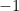 . Suppose
. Suppose  has a square root, and we call it
has a square root, and we call it 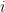 . If
. If 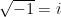 , then
, then  . If so, we can also answer the question that we have asked above:
. If so, we can also answer the question that we have asked above: 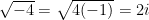 . As a matter of fact, we can generalize this operation for any negative number. If
. As a matter of fact, we can generalize this operation for any negative number. If  is positive, then
is positive, then 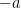 is a negative number. So,
is a negative number. So, 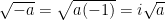 .
.
But what kind of number is 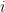 ? Surely, it is not a real number since we cannot locate it on the real number line. And, since we have all the real numbers and
? Surely, it is not a real number since we cannot locate it on the real number line. And, since we have all the real numbers and 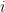 is not a real number, maybe, we should call
is not a real number, maybe, we should call 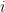 an imaginary number.
an imaginary number.
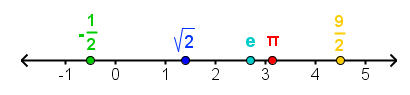
The Real Number Line
Imaginary numbers were ‘invented’ (or discovered if you prefer) because mathematicians wanted to know if they could think of square root of negative numbers, particularly, the root of the equation 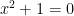 (that is,
(that is,  which is the same as finding the
which is the same as finding the 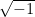 ). Just like the many ‘radical’ ideas in mathematics, it was not widely accepted at first, but eventually its invention proved to be very useful and has opened a lot of new ideas in mathematics.
). Just like the many ‘radical’ ideas in mathematics, it was not widely accepted at first, but eventually its invention proved to be very useful and has opened a lot of new ideas in mathematics.
In the next post in this series, we are going to discuss about the operations on imaginary numbers. .