Using Area to Prove the Arithmetic-Geometric Mean Inequality

February 16, 2012 GB High School Algebra, High School Mathematics, High School Number Theory

If we have real numbers $a$ and $b$ , we call $\frac{a + b}{2}$ the arithmetic mean (AM) and $\sqrt{ab}$ the geometric mean (GM) of $a$ and $b$ . In this post, we are going to examine the relationship of these two means.

To start off, let’s have a few examples. If $a = 3$ and $b = 12$ , then $GM = 6$ and $AM = 7.5$ ; if $a = 4$ and $b=16$ , then $GM = 8$ and $AM = 10$ ; if $a = 3$ and $b = 27$ , then $GM = 9$ and $AM = 15$ . What do you observe? Try a few example and see if your observations hold.

From a few examples above, and from your trials, you have probably observed that $GM \leq AM$ which means that $\sqrt{ab} \leq \frac{a + b}{2}$ for some positive real numbers $a$ and $b$ . This is actually true for all positive real numbers $a$ and $b$ . In the following discussion, we are going to use the concept of area to prove that the statement is true.

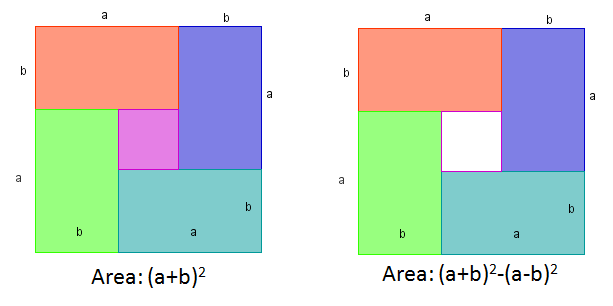
To begin the proof, we construct a square with side length $a + b$ made up of four rectangles and a square at the center (technically, a square is also a rectangle). Clearly, the area of each of the four rectangles is $ab$ , and the square at the center has are $(a - b)^2$ (Can you see why?). If we remove the square at the center, the remaining area is represented by the equation $(a + b)^2 - (a - b)^2=4ab$ . Note that $4ab$ is the total area of the four rectangles.

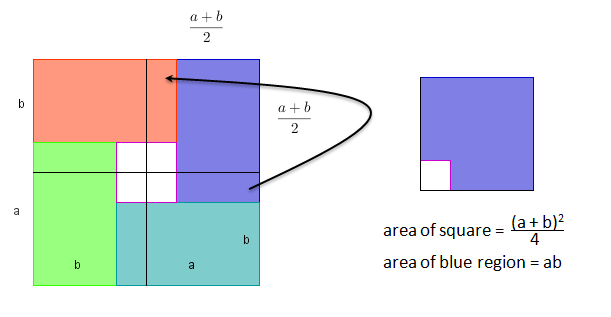
If we partition the large square into four (see figure below), each square will have side length $\frac{a+b}{2}$ and area $\frac{(a + b)^2}{4}$ . Notice that the remaining blue region on the lower-right square partition can be placed on the red region in the upper-right square partition since they are congruent (Can you prove it?). This results to the figure on the right. Since we did not remove anything from the blue region, the area of the blue region is equal to the area of the original rectangle which is $ab$ .

Clearly, the area of the blue region on the right is less than the area of the square partition. Therefore,

$ab < \frac{(a + b)^2}{4}$ .

Getting the square root of both sides, we have $\sqrt{ab} < \frac{a + b}{2}$ . However, if we let $a = b$ , then $\sqrt{ab} = a$ and $\frac{a +a}{2} = a$ . So if $a = b$ , the $\sqrt{ab} = \frac{a + b}{2}$ .