Visualizing the Difference of Two Squares

June 18, 2012 GB High School Algebra, High School Mathematics

Geometric objects are powerful representations that can be used to visualize algebraic properties of mathematical objects. Proofs without words are examples of such visual representations. In this post, we relate the difference of two squares to the areas of squares and rectangles.

The difference of two squares states that for all numbers $a$ and $b$ , $a^2 - b^2 = (a + b)(a-b)$ . The visual representation below, however, only covers the condition that $a^2 - b^2 \geq 0$ (Why?).

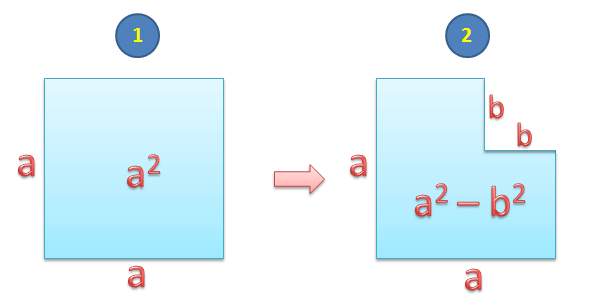
To proceed with the visual proof, we create a square with side length $a$ as shown in (1). Then, we cut a square with side length $b$ from its corner as shown in (2). Since the area of the larger square is $a^2$ and the area of the smaller square is $b^2$ , the area of the remaining figure is $a^2 - b^2$ .

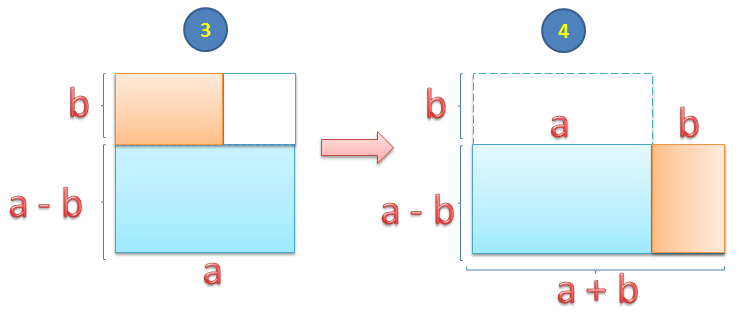
Next, we draw a horizontal line segment cutting the remaining figure into two rectangles as shown in (3). We change the color of the smaller rectangle for clearer representation, and move it to the right hand side as shown in (4).