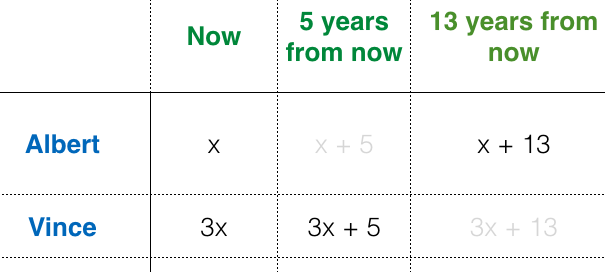Math Word Problems: Solving Age Problems Part 2
This is the second part of the 3-part installment posts on Solving Age Problems in the Math Word Problem Solving Series.
In this post, we continue with three more worked examples on age problems. The first part of this series can be read here.
PROBLEM 4
Janice is four times as old as his son. In years, she will be as three times as old as his son. What is Janice’s present age?
Solution
Let be the present age of Janice’s son and 4x be her age. According to the problem, in five years, she will be three times as old as her son.
In five years, Janice age will be and her son’s age will be
. If she is three times as old as her son, if we multiply her son’s age by
, their ages will be equal. That is,
.
Simplifying, we have giving us
. Therefore, the son is
years old and Janice is
years old.
Checking the Answer
The present ages of Janice and her son are and
respectively. Yes, she is four times as old as here son. In
years, Janice will be
and her son will be
. Since
is three times
, we are correct.
Problem 5
Vince is thrice as old as Albert. Vince age years from now will be equal to Albert’s age
years from now. What are their present ages?
Solution
Let be present age of Albert and
be the present age of Vince.
Vince’s age five years from now will be . This will be equal to Albert’s age
years from now which is
. So, we set up the equation
.
This gives us and
.
Checking the Answer
Left as an exercise.
PROBLEM 6
Anna is thrice as old as Karen and Nina is years older than Karen. In
years, the sum of Karen and Nina’s age will be
more than Anna’s age. What are their ages?
Solution
Let be Karen’s age,
be Anna’s age and
be Nina’s age. In three years, their ages will be
Karen:
Anna:
Nina: .
The sum of Karen and Nina’s age three years from now is . This is
more than Anna’s age three years from now. That means that if we add
to Anna’s age, her age will equal the sum of the ages of the two girls. That is,
This give us which gives us
.
Therefore, Karen is years old, Anna is
, and Nina is
.