School math, multimedia, and technology tutorials.
One of the most fundamental problems that gave birth to integral calculus was the calculation of areas bounded by curves. The Greeks used method of exhaustion to remedy this problem, particularly on finding the area of a circle. After Descartes’ and Fermat’s invention of Coordinate Geometry, algebraic solutions were utilized.
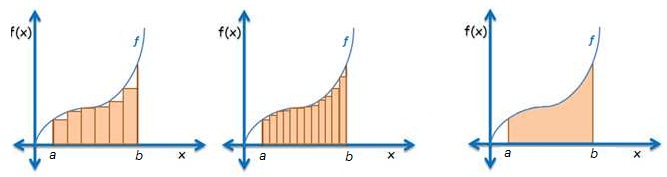
One of the strategies used to find the area under the function 
If you have used the GeoGebra Chrome App, you have surely noticed that there is no right click function. How do we solve this problem? GeoGebra expert Linda Fahlberg-Stojanovska gives us tips on how to remedy this problem in the tutorial below.
The Chrome App enables users to use GeoGebra on tablets and devices that do not support Java. Currently, GeoGebra developers are also developing real tablet apps particularly for the iPad and Android tablets.
This is the third part of the Solving Age Problems of the Math Word Problem Solving Series. In this post, we discuss more complicated age word problems.
Problem 7
Anna who is 
Solution
As years go by, the number of years added to Ben’s and Anna’s ages is the same. If we let the number of years that have gone by be 
Ben’s Age:
Anna’s Age:
Since in 
