The Golden Ratio and the Perfect Human Face
Mathematical beauty ranges from simple Youtube embedding to the elegance of tessellations and symmetry all the way to the complexity of fractals. In this post, we talk about the most interesting connection between beauty and mathematics, the mathematical beauty of the human face.
The Golden Ratio was used by architects, sculptors, and artists since the ancient times to express beauty in their work. Architectures based on Golden Ratio are considered pleasing to the human eye. The Pyramid of Egypt, the Pantheon, and the United Nations Building are just several examples of structures in Golden Ratio.
The Golden Ratio is based on the ratio of the length of a line segment divided into two parts. It is the division of a segment into two such that the ratio of the longer piece to the shorter piece is equal to the ratio of the longer piece to the entire segment. If the longer segment is and the shorter segment is
, the golden ratio is
.
The computation gives, , which mathematicians denoted with the Greek letter
.
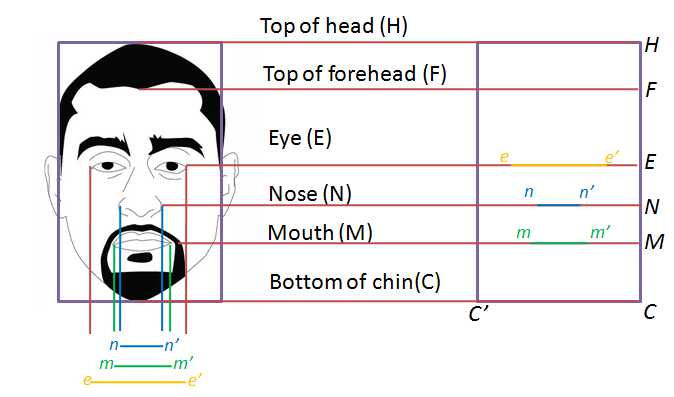
In the diagram above,
CC’ = Width of the human face
ee’ = Distance between outsides of the eyes
nn’ = Distance between the outsides of the nostrils
mm’ = Distance between the ends of the mouths.
The perfect human face contains the Golden ratio. In particular,
.
Of course, that is just from the mathematical point of view. Beauty is too complicated to be defined by just a single formula.
Note: This article was originally published in The Mathematical Palette on August 13, 2012.
Reference: Geometry of Art and Life, Matila Ghyka
Photo Credit: Kalid Albaih, Flickr