SSS Congruence Theorem and Its Proof

June 17, 2013 GB High School Geometry, High School Mathematics, Problem Solving and Proofs

Many high textbooks consider the congruence theorems (SSS Congruence Theorem, SAS Congruence Theorem, ASA Congruence Theorem) as postulates. This is because their proofs are complicated for high school students. However, let us note that strictly speaking, in Euclidean Geomtery (the Geometry that we learn in high school), there are only five postulates and no others. All of other postulates mentioned in textbooks aside from these five are really theorems without proofs.

In this post, we are going to prove the SSS Congruence Theorem. Recall that the theorem states that if three corresponding sides of a triangle are congruent, then the two triangles are congruent.

Before proving the SSS Congruence theorem, we need to understand several concepts that are pre-requisite to its proof. These concepts are isometries particulary reflection and translation, properties of kites, and the transitive property of congruence. If you are familiar with these concepts, you can skip them and go directly to the proof.

Isometry

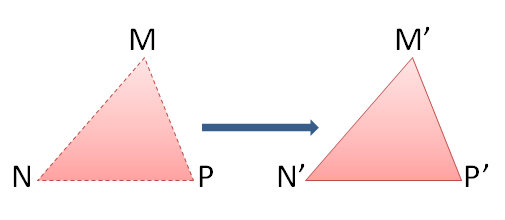
In the figure below, $\triangle MNP$ is slid to the right forming $\triangle M^\prime N^\prime P^\prime$ . Clearly, when you side a figure, the size and shape are preserved, so clearly, the two triangles are congruent.

Sliding or translation is a form of isometry, a type of mapping that preserves distance. In the isometry above, the preimage $\triangle MNP$ is mapped onto the image $\triangle M^\prime N^\prime P^\prime$ . Notice that there is a 1-1 mapping between the objects in the preimage and the objects in the image. Each object in the preimage has exactly one image. Also, each object in the image has exactly one preimage.

Properties of Kites

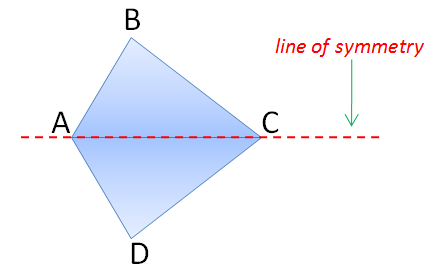
A kite is a polygon with two distinct pairs of congruent sides. In the figure below, $ABCD$ is a kite with $\overline{AB} \cong \overline{AD}$ and $\overline{BC} \cong \overline{CD}$ .

The diagonal $\overline{AC}$ is a line of symmetry of the kite. This means that $\triangle ABC$ mirrors $\triangle ADC$ . Mirroring an image or reflection preserves distance. This means that $\triangle ABC$ and $\triangle ADC$ congruent. Thus, we say that a kite is reflection-symmetric.

The Transitive Properties of Congruence

Let us recall the transitive property of equality of real numbers. It says that for any real numbers $a$ , $b$ , and $c$ , if $a = b$ and $b = c$ , then $a = c$ . This is also true in congruence. For any figure $P$ , $Q$ and $R$ ,

If $P \cong Q$ and $Q \cong R$ , then $P \cong R$ .

Now that we finished the prerequisite, we now prove the theorem.

The SSS Congruence Theorem

If in two triangles, three sides of one are congruent to three sides of the other, then the two triangles are congruent.

Proof

Given triangles $ABC$ and $DEF$ with $AB \cong DE$ , $AC \cong DF$ and $AC \cong DF$ .

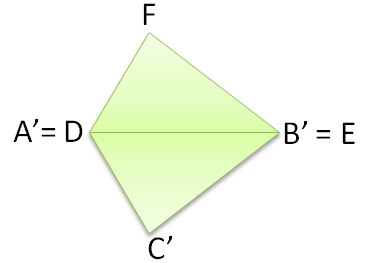
In proving the theorem, we will use the transitive property of congruence. We show that if a third triangle exists, and $\triangle ABC$ is congruent to it, then $\triangle DEF$ is also congruent to it. Let the third triangle be $\triangle A^\prime B^\prime C^\prime$ , an image of $\triangle ABC$ under an isometry.

To begin, since $\overline{AB} \cong \overline{DE}$ , there is an isometry that maps $\overline{AB}$ to $\overline{DE}$ . So, there is a triangle $A^\prime B^\prime C^\prime$ which is an image of $\triangle ABC$ that has a common side with $\triangle DEF$ .

Now, $\overline{AC} \cong \overline{A^\prime C^\prime}$ and $\overline{BC} \cong \overline{B^\prime C^\prime}$ . By the transitive property of congruence, $\overline {A^\prime C^\prime} \cong \overline{DF}$ and $\overline{B^\prime C^\prime} \cong \overline{EF}$ . Therefore, $\triangle A^\prime B^\prime C^\prime$ and $\triangle DEF$ form a kite. Since this kite is reflection-symmetric over line $DE$ , $\triangle DEF$ is a reflection of $\triangle A^\prime B^\prime C^\prime$ which means that $\triangle A^\prime B^\prime C^\prime \cong \triangle DEF$ .

So, if the three pairs of sides of $\triangle ABC$ can be mapped onto $\triangle DEF$ by an isometry, by the definition of congruence, $\triangle ABC \cong \triangle DEF$ . This prove the SSS Congruence Theorem.

Reference: An old edition of Geometry (University of Chicago School Mathematics Project)

2 comments properties of a kite polygon, sss congruence proof, sss congruence theorem, sss triangle congruence proof, transitive property of congruence, triangle congruence

SSS Congruence Theorem and Its Proof

Isometry

Properties of Kites

The Transitive Properties of Congruence

The SSS Congruence Theorem

Leave a ReplyCancel reply