Calculating The Value of Pi
We have met the number or the approximation of pi (written as
) in our good old elementary school days. In fact, we have used it a countless number of times in mathematical computations. Most of us have used it when calculating the area of a circle or volume of a sphere, but only a few probably know that it appears in numerous branches of mathematics and even in other sciences.
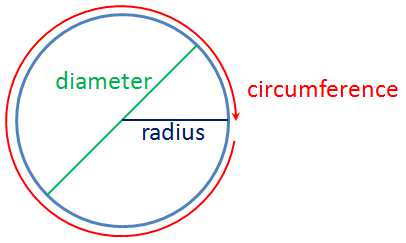
The number is the ratio of the circumference of a circle to its diameter. What does that mean? It means that if we measure the circumference of a circle and its diameter and divide them, the quotient is “three point something.” Now that three point something is
. What is amazing is that this is always true even if the circle is a big as a planet or as small as an atom.
Pi is an irrational number; it cannot be written as fraction. If you are wondering why you have seen it as fraction before in some books, for instance, such values are only approximations.
is also the circumference of a circle with diameter 1 unit. As shown in the animation in the second figure, when a circle with diameter 1 unit is rolled, the length of its circumference is
.
Many mathematicians wanted a more accurate value of . Archimedes, for instance, inscribed and circumscribed polygons on a circle to find a more precise value. Since the circumference of a circle with diameter 1 unit is
, increasing the number of sides of the polygons will give a perimeter closer to the circumference.
Archimedes approximated in 250 BC, while the Chinese mathematician Lu Hui approximated it
in 480 AD. Francois Viete approximated it up to 10 decimal places in 1593 and Ludolph van Ceulen approximated it up to 35 decimal places. Many attempts to calculate manually had been made since then; the most notable was that of William Shanks. Shanks calculated
up to 707 places, but his calculation was only up to 527 places correct.
Due to the invention of modern computers, the computation of had been done electronically. In 1947, D. F. Ferguson calculated
up to 1120 places using a desktop calculator. In 1949, the first electronic computer ENIAC calculated
up to 2037 places. Since then, more precise values of
were calculated using electronic computers (see chronology).
The latest calculation of as of this writing was done by Alexander Yee and Shigeru Kondo. In 2011, after almost a year of electronic computation, they calculated
up to 10 trillion digits.
***
References: The Story of Mathematics, Wikipedia