On Equations of Intersecting, Coinciding, and Parallel Lines

When we have two lines on a plane, there are three possibilities:

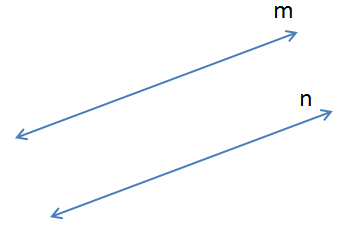
• the lines will never meet (parallel)
• the lines will meet at one point (intersecting)
• the lines will meet at infinitely many points (coinciding).

As for the third case, coinciding means that lines which are on top of each other.

In Algebra, we have learned that a line can be represented with an equation. The equations which represent lines are called linear equations. We have learned that linear equations can be represented by , where and are real numbers.

We can examine the three cases mentioned above in terms of equations. Can we determine if lines are parallel, intersecting, or coinciding based on equations only? 

Parallel Lines

What we know about parallel lines is that they have same slope. In linear equations, recall that in the slope-intercept form , is the slope of the line and is the y-intercept. The y-intercept is the point in the y-axis where the line intersects. Therefore, we will know that two lines are parallel if they have the same value for when the equations are of the form . For example, the lines with equations

and .

are parallel lines because both of them have .

But what if they have the same b? Are they still parallel?

If we have two lines having the same slope and intersect the same point on the y-axis, then they are practically the same line (Can you visualize why?). Therefore, for distinct lines to be parallel, their slope (m) must be equal and their y-intercept (b) must be different.

Exercise: Give equations of lines that are parallel to the following lines.

1. y = 4x – 5
2. 3x + y – 7 = 0

Intersecting Lines

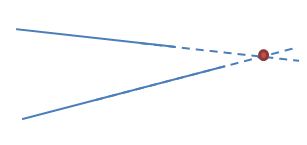
If two lines have different slopes, then definitely they will meet at a certain point. You can imagine this by drawing two line segments that are not parallel on a board (the intersection may be outside the board). If you extend the two segments on one side, they will definitely meet at some point as shown below.  The extension of the line segments are represented by the dashed lines.

Therefore, if two lines on the same plane have different slopes, they are intersecting lines.

Exercise: Give equations of lines that intersect the following lines.

1. y = 7x + 2
2. 3x + 8y – 7 = 0

Coinciding Lines

As discussed above, lines with the same equation are practically the same line. Therefore, to be able to distinguish coinciding lines using equations, you have to transform their equation to the same form (e.g. slope-intercept form). For example, the lines 3x + y = 5 and 3x = 5 – y are coinciding lines because they both can be transformed to y = -3x + 5. So, if two equations can be transformed to one form and they are equal, they are coinciding lines.

But how about 3x + 8y = 12 and 6x + 16y = 24? They are coinciding lines. Can you see the relationship between the two equations?

We will continue our discussion the next post.