Mathematical Tasks: Number of Solutions and Answers
Different types of mathematical tasks let us tests the various skills of students. Close ended tasks let us test students basic knowledge of facts and procedures, while open-ended tasks lets us elicit various solutions answers. In the book Mathematical Thinking, Isoda and Katagiri classified mathematical tasks into three types:
Type 1: one solution, one answer
Type 2: many solutions, one answer
Type 3: many solutions, many answers
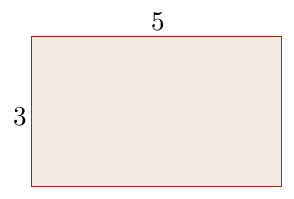
Examples of such problems are shown below. The first task is a Type 1 task, or a task with one solution and one answer. Students who have already learned how to calculate the area of rectangles can just use the formula to calculate the area of the rectangle.
Type 1: Find the area of the rectangle below.
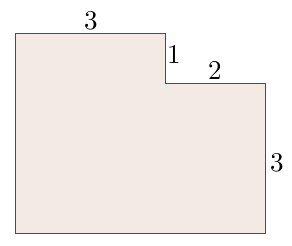
The second task is a Type 2 task, a task with many solutions but only one answer.
Type 2: Find the area of the figure below.
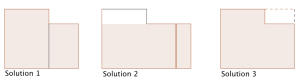
Students can divide the figure into two rectangles and add their areas (Solution 1), cut the figure and create another rectangle (Solution 2), and “complete” the rectangle and subtract the area of the smaller rectangle (Solution 3). All these solutions lead to only one answer.
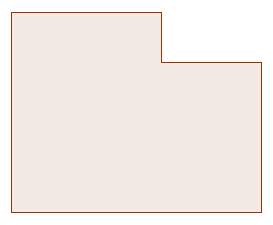
Using the same figure above, if no lengths are given, then the task becomes a Type 3 task, or a task with many answers and many solutions. Students can measure or estimate the lengths of the sides and can have various answers. Of course, they can still use the three methods stated above. The focus of this problem is not the answer but the methods of getting the area.
Type 2: Find the area of the figure below.
It can also be noted that the Solution 1 and Solution 3 can be generalized; they can be used to compute the area of the figure for any side lengths. Solution 2 on the other hand cannot: the sides of the partitioned triangle must coincide, so at least one of the sides should be equal.