The effect of the sign of the slope in y = ax

November 16, 2015 GB High School Algebra, High School Mathematics

A linear function is a function whose equation is of the form $y = ax + b$ . We separate the discussion about it into two parts: $b = 0$ and $b \neq 0$ . In this post, we only discuss the graph of $y = ax + b$ where $b = 0$ . We discuss the effect of the sign of the slope in $y = ax$ .

If we let $b = 0$ , the equation $y = ax + b$ becomes $y = ax + 0$ or simply $y = ax$ .

Notice that if $x = 0$ , then $y = ax = a(0) = 0$ . This means that the graph contains the point with coordinates $(0,0)$ . Therefore, $y = ax$ passes through the origin.

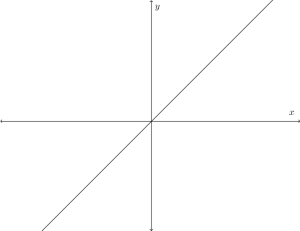
Generalization 1: The graph $y = ax$ passes through the origin.

We now examine the effect of the values of $a$ . There are three cases: $a = 0$ , $a > 0$ , and $a < 0$ .

Case 1: $a = 0$

If $a = 0$ , then $y = 0(x) = 0$ . This means that for all values of $x$ , the value of $y = 0$ . This gives us the horizontal line $y = 0$ .

Case 2: $a > 0$

If we let $x > 0$ , then $ax > 0$ since $a > 0$ . That is, we multiplied a positive number $a$ by a positive number $x$ which means that their product is positive. In effect, if $x > 0$ , then $y >0$ . This only means that the graph passes through the first quadrant.

If we let $x < 0$ , then $ax > 0$ since $a > 0$ . That is, we multiplied a positive number $a$ by a negative number $x$ which means that their product is negative. In effect, if $x < 0$ , then $y < 0$ . This only means that the graph passes through the third quadrant.

So, the graph $y = ax$ where $a > 0$ passes through the origin (Generalization 1) and parts of it are on the first and third quadrant.

Generalization 2: If $a > 0$ , the graph $y = ax$ passes through the origin, the first quadrant, and the third quadrant.

Case 3: $a < 0$

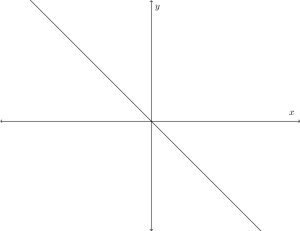
If we let $x > 0$ , then $ax < 0$ since $a < 0$ . That is, we multiplied a negative number $a$ by a positive number $x$ which means that their product is negative. In effect, if $x > 0$ , then $y < 0$ . This only means that the graph passes through the fourth quadrant.

If we let $x < 0$ , then $ax > 0$ since $a < 0$ . That is, we multiplied a negative number $a$ by a negative number $x$ which means that their product is positive. In effect, if $x < 0$ , then $y > 0$ . This only means the graph passes through the second quadrant.

So, the graph $y = ax$ where $a < 0$ passes through the origin (Generalization 1) and parts of it are on the second and fourth quadrant.

Generalization 3: If $a < 0$ , the graph of $y = ax$ passes through the origin, the first quadrant, and the third quadrant.

In the next post, we are going to relate the increase and decrease of a in the graph of the function y = ax.

Leave a comment graph of linear functions, linear functions, sign of the slope, y = ax

The effect of the sign of the slope in y = ax

Leave a ReplyCancel reply