Constructing segments with irrational lengths
Since rational numbers can be expressed as fractions (or ratio of two integers), rational numbers can be easily located on the number line using compass and straightedge construction. In principle, a segment of any length can be divided into any number of parts; hence, it is possible to locate any rational number on the number line. Irrational numbers, on the other hand, cannot be expressed as ratio of two integers, so the big question is:
How do we locate irrational numbers on the number line?
The question above is equivalent to: “How do we construct a segment with irrational lengths?”
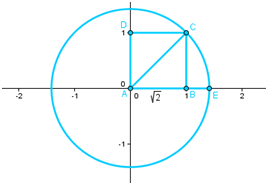
It is easy to locate some irrational numbers on the number line even with compass and straightedge construction. The irrational can be located by constructing square ABCD (Figure 1), getting the diagonal AC, and constructing a circle with radius AC. It follows that the length of AE is
, and the coordinates point E are
.
It is also apparent that the easiest way to construct segments with irrational lengths is by constructing diagonals of rectangles. In Figure 2, OB, OC and OD have lengths ,
, and
respectively. More complicated construction is required to construct other irrational lengths,
for instance, which is the length of EH. » Read more