Calculus and Analysis Archives - Page 6 of 7

Derivative and the Maximum Area Problem

February 24, 2010 GB Calculus and Analysis, College Mathematics, High School Calculus

Note: This is the third part of the Derivative Concept Series. The first part is The Algebraic and Geometric Meaning of Derivative and the second part is Derivative in Real Life Context.

Introduction

The computation of derivative is often seen in maximum and minimum problems. In this article, we will discuss why do we get the derivative of a function and equate it to 0 when we want to get its maximum or minimum. To give you a concrete example, let us consider the problem below.

Find the maximum area a rectangle with perimeter 10 units.

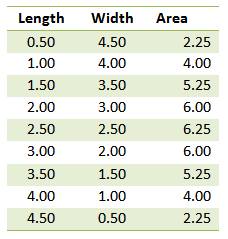
Without using calculus, we can substitute values for the rectangle’s length, compute for its width and its corresponding area. If we set the interval to 0.5, then we can come up with the table shown in Figure 1.

Figure 1 - Table showing the length, width, and area of a rectangle with perimeter 10.

Looking at the table above, we can observe that a rectangle of length of 2.5, a square, has the maximum area. If we have prior calculus knowledge, however, we know that whatever the value of our perimeter, a square having the given perimeter will always have the maximum area.

Using elementary algebra, if we let $x$ be the width of our rectangle, it follows that the length is $5-x$ . Let $f(x)$ be the area of the rectangle. In effect, the area of the rectangle is described by the equation $f(x) = 5x - x^2$ . We want to maximize the area, which implies that we want to find the maximum value of $f(x)$ .

Figure 2 – A rectangle with Perimeter 10 and width x units.

In elementary calculus, to compute for the maximum value of $f(x)$ , we get its derivative, which is equal to $5 - 2x$ , which we will denote $f'(x)$ . We then equate the $f'(x)$ to $0$ resulting to the equation $5-2x=0 \Rightarrow x = 2.5$ which is exactly the maximum value in the table above.

Derivative and Equation to 0

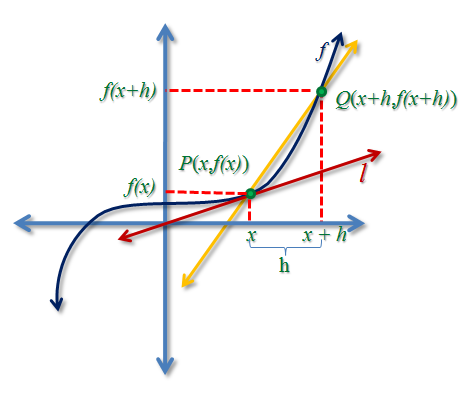
In the article the Algebraic and Geometric Meaning of Derivative, we have learned that the derivative of a function is the slope of the line tangent to that function at a particular point. From elementary algebra, we also have learned the properties of slopes. If a line is rising to the right, the slope is greater than 0; if the line is rising to the to the left, then the slope is less than 0. We have also learned that a horizontal line has slope 0 and the vertical line has an undefined slope.

Figure 3 – Properties of slope of a straight line.

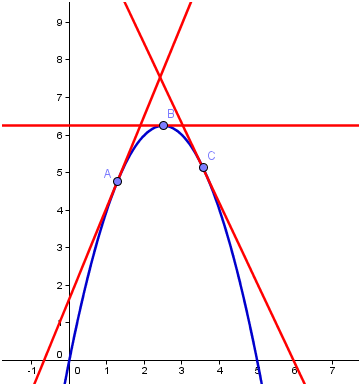
In the problem above, we calculated by getting the derivative (the slope of the line tangent to a function at a particular point) and equate it to $0$ . But a line with slope $0$ is a horizontal line. In effect, we are looking for a horizontal tangent of $f(x) = 5x-x^2$ . To give a clearer picture let us look at the graph of $f(x) = 5x - x^2$ .

Figure 4 – Tangent lines of 5x – x2.

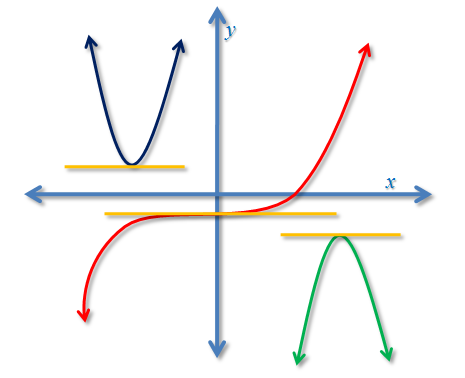
From the graph it is clear that the maximum point of the function is where the tangent line (red line) horizontal. In fact, there are only three possible cases that tangent line could be horizontal as shown in Figure 5: first, the minimum of a function (blue graph); second, the inflection point (red graph); and the third is the maximum of the function (green graph).

It should also be noteworthy to say that all the ordered pairs (length, area) or(width, area) in Figure 1 will be on the blue curve in Figure 4.

Figure 5 – Cases of a graph where the tangent is horizontal.

The derivative has many applications and it is seen in many topics in calculus. In the next Derivative Tutorial, we are going to discuss how the derivative is used in other context.

Summary

The derivative of a function is the slope of the line tangent to a function at a particular point.
The horizontal line has slope zero.
In solving maxima and minima problems, we get the derivative of a function and equate to zero to get the minimum or maximum. We do this because geometrically, we want to get the line tangent to a function at a particular point that is horizontal.

2 comments calculus maxima and minima problems, derivative of a function, elementary calcululucs, horizontal tangent line, line tangent to a function, maximum area, maximum of a function, minimum of a function, negative and positive slopes, point of inflection, properties of slope, zero and undefined slope

Derivative in Real Life Context

February 19, 2010 GB Calculus and Analysis, College Mathematics

Note: This article is the second part of the derivative concept series. The first part is The Algebraic and Geometric Meaning of Derivative and the third part is Derivative and the Maximum Area Problem.

If we change the labels of the Figure 2 in the The Algebraic and Geometric Meaning of Derivative article – its x-axis to time and the y-axis to distance – the graph of the secant line is the difference in distance $y_2 - y_1$ = 100 km – 50 km over the difference in time $x_2 - x_1$ = 10:00 – 8:00. This is shown in the figure below. This is equivalent to 50 km/2 hrs or 25 km/hr. From the computation above, it is clear that the interpretation of the slope of the secant line is the total distance over the total time or the average speed.

On the other hand, the slope of the tangent line is the speed of the bicycle at exactly 4 o’clock. At exactly 4:00 o’clock the bicycle was traveling 50 km per hour, a lot faster than its average speed. Now, this is reasonable because in real life, the speed of travel is not always constant. The slope of the tangent line or the speed of travel at a particular point is called the instantaneous speed.

We have also observed from the previous article that as Q approaches P, the secant line’s approximation of the tangent line becomes better and better. This means that as Q approaches P, the average speed becomes closer and closer to the instantaneous speed at P.

2 comments derivative formula, derivative in real life context, first derivative, interpretation of derivative

The Algebraic and Geometric Meaning of Derivative

February 15, 2010 GB Calculus and Analysis, College Mathematics

Note: This is the first part of the Derivative Concept Series. The second part is Derivative in Real Life Context and the third part is Derivative and the Maximum Area Problem.

***

If we want to get the slope of a line, we need two points. Suppose the points have coordinates $(x_1,y_1)$ and $(x_2,y_2)$ , we have learned that the slope is described by the formula $\displaystyle\frac{y_2-y_1}{x_2-x_1}$ .

In Figure 1, we have line $l$ tangent to the function $f$ at point $P$ where the coordinates of $P$ are $(x,f(x))$ . The problem that gave birth to calculus is getting the slope of this tangent line. There is, however, a problem. We need two points to compute for the slope but we have only one point.

Note that the word tangent in this problem is different from the definition of tangent on a circle because it is clear that line $l$ will intersect the graph in more than one point.

Figure 1 - Line l tangent to the function f at point P.

Using the concept of limits we can remedy this problem. First, we create point $Q$ with x coordinate $h$ units to the right of the x-coordinate of $P$ . We then draw line $PQ$ , a secant line to the function $f$ .

Figure 2 - A secant line is drawn through P.

In effect, the coordinates of $Q$ would be $(x+h, f(x+h))$ and it is clear that the slope of the secant line $PQ$ is described by the formula

$\displaystyle\frac{f(x+h)-f(x)}{x+h - x} = \frac{f(x+h)-f(x)}{h}$

If we want to approximate the slope of the tangent line, it is reasonable that we move $Q$ towards $P$ with $P$ fixed. Click here to explore the diagram above using GeoGebra.

From the GeoGebra exploration above, if we move $Q$ towards $P$ , we observe the following:

1.) The value of $h$ approaches $0$ .

2.) The inclination of the secant line approaches the inclination of the tangent line.

3.) The slope of the secant line approaches the slope of the tangent line.

4.) If point $Q$ coincides with point $P$ , then the slope of the secant line and is equal to the slope of the tangent line.

If we let $m$ be the slope of the secant line and $f'(x)$ be the slope of the tangent line, focusing on observations 1 and 4, we can say the following equivalent statements:

The limit of the slope of the secant line $m$ as $Q$ approaches $P$ is equal to $f'(x)$ .
The limit of the slope of the secant line $m$ as $h$ approaches $0$ is equal to $f'(x)$ .
The limit of $\displaystyle \frac{f(x+h)-f(x)}{h}$ as $h$ approaches $0$ is equal to $f'(x)$ .

Using the limit notation, we can say that

$f'(x) = \lim_{h \to 0} \displaystyle\frac{f(x+h)-f(x)}{h}$

From the above discussion, we can see that the derivative of a function at a particular point is the slope of the line tangent to that function at that particular point.

In the next post, we will discuss the meaning of derivative in real life situations.

7 comments derivative formula, differential calculus, differentiation, first derivative, limits, secant line, slope, tangent line

« 1 … 4 5 6 7 »