Category: Number Theory

Clock Arithmetic and Modular Systems Part 2

College Mathematics, Number Theory

This is the second part of the Introduction to Modular Systems Series. Please read the first part before proceeding.

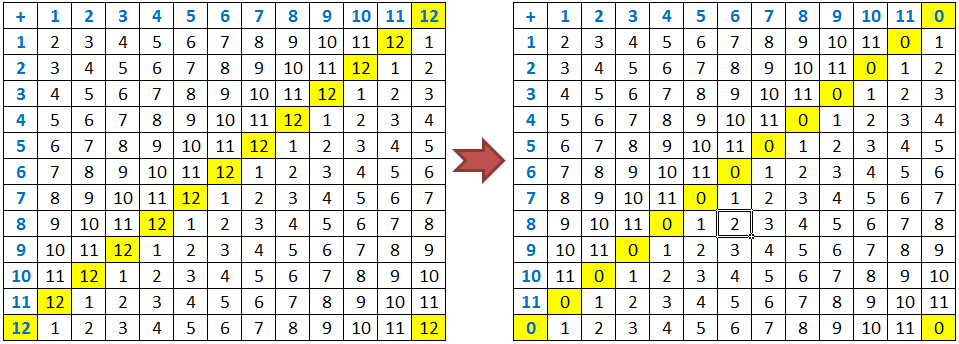
Last Monday, we have learned a number system that uses numbers on the 12-hour analog clock. We have performed addition using these numbers and discovered that in that system, 12 behaves like 0. We have also observed that to add large numbers, we need to divide the number by 12 and get the remainder.

modulo-12

Recreating the table by replacing 12 with 0 gives us the second table in the figure above. As we can see, in this new number system, we have digits 0 through 11 as opposed 0 through 9 in the number system that we use everyday (the decimal number system).

In this new system, we have observed that there is a certain  number where numbers wrap around. The wrap around number is called the modulo. The modulo of our “clock number system” is 12, so we call it modulo 12. » Read more

9 comments , , ,

Introduction to Clock Arithmetic and Modular Systems

College Mathematics, Number Theory

Most of us are familiar with 12-hour analog clocks. They are numbered 1 through 12; they have hour, minute, and second hands. In this post, we are going to experiment clock arithmetic — we are going to perform addition using the numbers on the clock.

clock arithmetic

Let us think about the following questions.

  • What if we add 3 hours after 8:00?
  • What if we add 2 hours after 3:00?
  • What if we add 4 hours after 11:00? » Read more
5 comments , , ,

Divisibility by 5 and 10

Number Theory

This is the third post in the Divisibility Rules Series.  The first was about divisibility by 2 and the second was about divisibility by 4.  In this post, we discuss divisibility by 5 and 10.

If we skip count by 10, we will immediately realize that the numbers always end in zero: 10, 20, 30, 40, and so on. It is clear that all multiples of 10 end in 0; therefore,  a number is divisible by 10 if the ones digit is 0.

On the other hand, if we skip count by 5, then we have 5, 10, 15, 20, 25, 30 and so on. Notice that if we add 5 to a number whose ones digit is 5, the ones digit of the sum is 0. Similarly, any number whose ones digit is 0 added to 5, the ones digit of the sum is always 5.  Hence, we conclude that a number is divisible by 5, if the ones digit is either 5 or 0.

From here, we can see clearly that all numbers that are divisible by 10 are also divisible by 5.

4 comments , , , ,
1 2 3 4 … 6