As a preparation for more posts on probability, statistics, permutations and combinations, we familiarized ourselves last week with the different terminologies and notations of probability. We continue in this post by studying set terminologies, notations, and operations. Note that this is also the third post in the Set Primer Series; the first and second are Introduction to Sets and Subset: a set contained in a set.
Universal Set
The universal set is the set that contains all the elements under discussion. If we talk about the letters in the English alphabet, then the universal set contains all the 26 letters. In set theory, universal set is usually denoted by 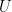 .
.
In the following discussion, we let 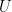 be the set of integers,
be the set of integers, 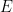 be the set of even integers, and
be the set of even integers, and 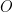 be the set of odd integers. The following are the common operations on sets.
be the set of odd integers. The following are the common operations on sets.
Intersection
If sets  and
and  have elements in common they form a set written as
have elements in common they form a set written as  . This is the intersection of
. This is the intersection of  and
and  .
.

Example: If we let 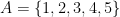 and
and 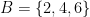 then
then  . » Read more
. » Read more