The 3 Ancient Construction Problems
Problems about construction using compass and straightedge preoccupied mathematicians for 2000 years. The first three postulates of Euclid’s Elements (300 BC) involve constructions and the first proposition was about the construction of an equilateral triangle. Constructions of other regular polygons were solved, but the heptadecagon (17-gon) proved to be difficult. It was only solved by Carl Friedrich Gauss in 1796 when he was just 19 (see the following animation).
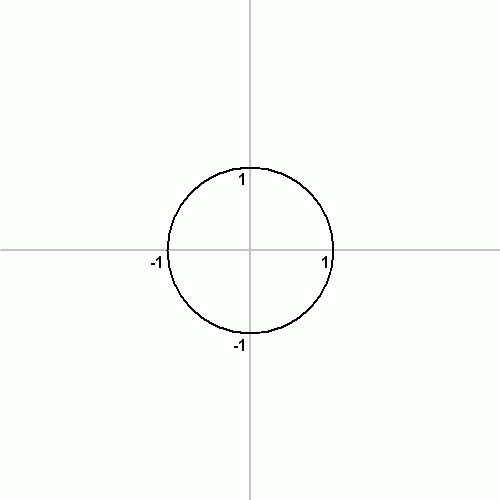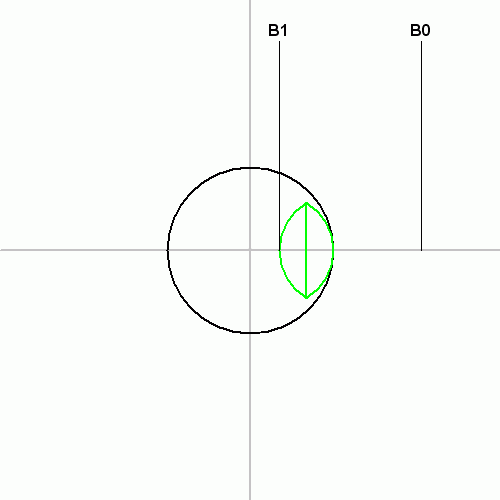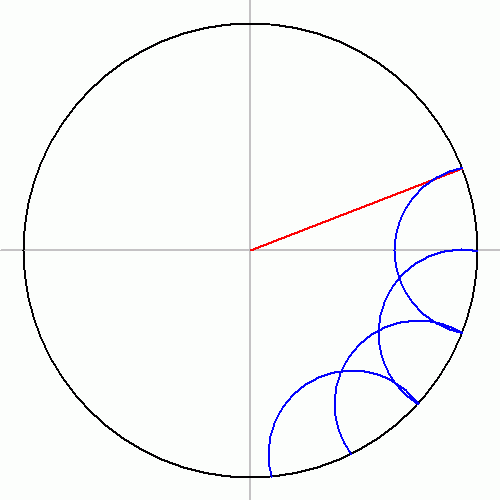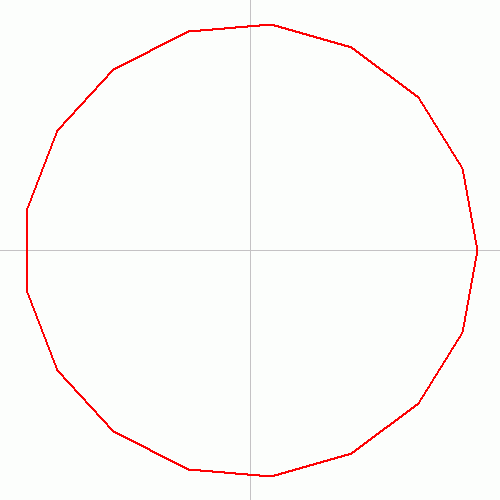
Aside from the heptadecagon problem and other construction problems, numerous mathematicians attempted to solve the three most difficult ancient construction problems: trisection of any given angle, duplication of a cube, and squaring the circle. » Read more
or the approximation of pi (written as 
) in our good old elementary school days. In fact, we have used it a countless number of times in mathematical computations. Most of us have used it when calculating the area of a circle or volume of a sphere, but only a few probably know that it appears in 
unfortunate among all the mathematicians. His father committed suicide; he failed the entrance exam at