Category: High School Algebra

Slope Concept 1 – Understanding the Basic Concepts of Slope

High School Algebra, High School Mathematics

Note: This is the first part of the the Slope Concept Series. The sequels of this article are Part II – Slope of the Graph of a Linear Function and Part III – Slopes of Vertical and Horizontal Lines.

***

The slope is known to be the steepness of a line.  Sometimes it is described as “rise over run,” If we are on point A, we go up 4 units and we go right 5 units (see Figure 1) then our rise is 4 and our run is 5. Let us mark our new location B. Notice that the order of movements does not matter. We can also go 5 units right and 4 units up and you will still be in B (see Figure 2).

If we do our movement in the coordinate plane starting from the origin, our rise would be our vertical movement (change of movement with respect to the y-axis) and our run would be our horizontal movement (change of movement with respect to the x-axis). In Figure 2, segment AB has rise 4 and run 5.  Thus, the slope of segment AB is \displaystyle\frac{4}{5}.  In general, slope in the coordinate plane is described as the change in y over the change in x.

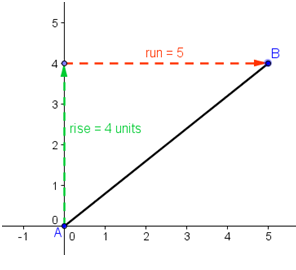
Figure 1 - Segment AB with rise 4 units and run 5 units.

The slope of a line (or a segment) may also be described as the angle it makes with a horizontal line.  Technically speaking, it is a counterclockwise rotation with the line starting from a horizontal position about a point which is located on that line, or the origin our case.  In Figure 2, \theta is the angle measure AB makes with the horizontal axis of the rectangular coordinate plane, or the amount of rotation from AB’ to AB about A.

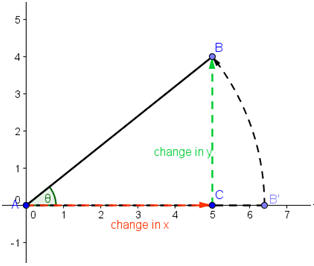
Figure 2 - Counter-clockwise rotation of AB to AB' about A.

Looking at triangle ABC, since the given sides are the side adjacent and the side opposite to \theta, we can use the definition of tangent to compute for the value of \theta. Recall from trigonometry that the definition of a tangent of an angle of a right triangle is equal to the quotient of the length of the side opposite to it (change in y) and the length of the side adjacent to it (change in x). Now, this is precisely the definition of slope. From here, we can conclude that the angle that a line makes with a horizontal line is the same as the slope of that line. As a consequence \tan(\theta) = \displaystyle\frac{4}{5} in radian measure (or approximately 38 degrees) is the slope of the line.

Figure 3 - Triangle ABC with Slope 4/5.

If we examine the value of \theta, it is clear that when \tan(\theta) is 0 degrees, the line is horizontal since there is no (zero) change in y. Algebraically, this makes the numerator of the fraction change in y 0 which implies that the slope of any horizontal line is 0.

If the line is vertical, there is no (zero) change in x. That makes the denominator of the fraction change in x 0. Of course, we know that anything divided by 0 is not defined. As a consequence, slope of a vertical line is undefined.

In the continuation of this article, we will discuss further about the properties of slope. We will discuss why the slope of a straight line is constant. We will further discuss zero, undefined, negative and positive slopes. We will also discuss how the concept of slope helps in solving calculus problems and how it is used to determine the behavior functions.

9 comments , , , , , , , , , , , , , , ,

Letters, Variables and Algebraic Expressions

High School Algebra, Pedagogy and Teaching

Letters and symbols represent numbers and objects in mathematics. However, many of us are probably not aware that we use them in different ways.  Below are the different uses of letters and symbols in algebra.

1.)  Generalized Arithmetic – symbols/letters stand as “pattern generalizers”

Example 1 : 3 + 5 = 5 + 3 is generalized as a + b = b + a

Example 2 : – 2 · 3 = -6, – 1 · 5 = – 5 is generalized as – x · y = -6

Example 3: y = mx + b

2.) Unknowns – symbols/letters are used as place holders of a specific value

Example 1 : 2x + 3 = 15

Example 2 : 3x = 4

3.)  Variables – symbols/letters represent a varying quantity

Example 1 : y  = 5x + 3

Example 2 : y = 2x

4.) Constants – symbols/letters with a constant value

Example 1 :  ≈  3.1416

Example 2 :  e ≈  2.71828

4 comments , , , , , , , ,

Introduction to the Concept of Functions

High School Algebra, High School Mathematics

Problem: A cube is painted on all faces and cut into smaller cubes of the same size. Investigate the number of painted faces of the smaller cubes.

Discussion

In Figure 1, shown are the cubes with side lengths two units and three units. The light blue cube has been painted and cut into eight smaller unit cubes, while the yellow cube has been painted yellow and cut into 27 smaller unit cubes. To avoid confusion, we will simply call the bigger or uncut cubes “cube”and the smaller cubes “unit cubes”.

How many unit cubes can be formed from a painted cube with length 4 units? 5 units? n units?

Figure 1 – Cubes with side lengths 2 and 3 cut into unit cubes.

Before scrolling down, investigate the number of painted faces of each yellow unit cube. In Figure 2, the unit cubes have been drawn from different perspectives to make visualization easier.

How many cubes are there with 3 painted faces? 2 painted faces? 1 painted face? 0 painted face?

Figure 2 – Cube cut into 27 unit cubes shown in different perspectives.

Without drawing, can you determine the number of painted faces of a cube with side length 4 units? How about 5 units? 6 units?

Challenge: Find a formula for the number of unit cubes 3 painted faces, 2 painted faces, 1 painted face and 0 painted face given a side length n units.

To determine how many unit cubes are painted given a particular size, it will help us if we know the properties of a cube. Let us recall that a cube has 8 vertices, 6 faces and 12 edges.

Figure 3 – Parts of a cube.

For the sake of discussion, we will name and color the unit cubes (see Figure 4) and group them depending on their positions – whether they are at the edges, vertices or faces of the cube.

  • Vertex Cubes (Red) – are the unit cubes located at the vertices of the cube. It is evident only 3 of their faces are painted.
  • Edge Cubes (Green) – are the unit cubes located at the 12 edges of the cube. Note that only two of their faces are painted.
  • Wall Cubes (Blue) – are the unit cubes at the faces of the cube. We will call the wall cubes because we will use the word “face” in another context.
  • Core Cubes (No color) – are cubes that are at the core of the cube that was not painted.

Figure 4 – The cube showing number of painted faces depending on their positions.

From Figure 4, it is clear that vertex cubes have 3 painted faces, edge cubes have 2 painted faces, wall cubes have 1 painted face and core cubes have no painted face.

Extending this type of grouping to cubes of larger side lengths, a pattern can be seen as shown in the table below. The calculation for the number of cubes can be generalized.

Figure 5 – Table showing the relationship of the number of painted faces given the cube’s sidel length.

Let us make the following definitions:

a = number of core cubes of an cube with side length n

b = number of wall cubes of a cube with side length n

c = number of edge cubes of a cube with side length n

d = the number vertex cubes with side length n

then

a = (n – 2)3 = n3 – 9n2 + 27n – 27

b = 6(n-2)2 = 6n2 – 24n + 24

c = 12(n-1) = 12n- 12

d = 8

That means that we have created a formula for finding the number of painted faces no matter how large it is. For example, if we want to find the number of wall cubes in from a cut cube with length 100 units, then there are a = 6(100)2 – 24(100) + 24 = 57624 wall cubes.

Question: If m is the volume of the cube before it was cut, then how can you express m in terms of a,  b, c and d?

Let us consider first the equation c = 12(n-1) = 12n – 12. Note that for each side length n, there is a corresponding number of edge cubes denoted by c. And there is only one c. For instance, if n = 3, there is no other value for c except 24. And clearly, this is true for all values of n.

If for each n there is exactly one corresponding c, then we say that c is a function of n.  Hence, we describe what a function means:

A function is a relationship between two sets where for every element of the first set, there is exactly one corresponding element in the second set.

In our case, our first set is the side length of the cube which is n, and our second set is the number of edge cubes that we denoted by c.   In general, if we have set A and set B, for every element in A, there is exactly one corresponding element in B.

The symbol f(x) is read as “f of x” and is usually used as a notation of a function.

We now denote the functions a as f(x), b as g(x), c as h(x) and d as k(x).

We will now graph our functions in the xy plane. The graphs of these functions are shown in Figure 6. The dots represent the ordered pairs and the dashed lines and curves are the lines that we will be formed if we will let x be the set of real numbers instead of integers.

Figure 6 – The points and the trendlines of the graphs of f(x), g(x), h(x) and k(x).

Summary

In this article, we have learned the following:

  • A function is a relationship between varying quantities.
  • A function is a relationship between two sets where for each element in the first set, there is exactly one corresponding element in the second set.
  • A function maybe represented as a table, set of ordered pairs such as (3,8), (4,8), (5,8), equations and graphs.

In the sequel of this article, we will discuss more about the basics of functions and its properties, so keep posted.

Leave a comment , , , , , , , , , , , , , , , , ,
1 … 26 27 28 29 30 31