Category: High School Algebra

Compound Interest and the Irrational Number e

High School Algebra, Math in Real Life

Suppose we borrow Php* 1.00 from a loan company at an interest rate of 100% a year, then after a year we would have to pay Php 2.00. We have learned from elementary school mathematics that to get the interest, we have to multiply the principal by the rate.  Just in case, we already have forgotten, the computation to calculate the interest is shown below.

Figure 1 – Computation of the Interest of 1.00 given a rate of 100% a year.

*Php stands for Philippine pesos, the currency in my country.

The situation above is an example of a simple interest problem.  Simple interest is calculated by multiplying a fixed interest rate to a principal amount over a fixed period of time.

There are several scenarios that could happen in loaning money. Most of the loan companies accept early payments; some allow the borrowers to re-borrow the money, and some apply interests to amount payable just like re-borrowing money. Let us see what happens in both scenarios.

Scenario 1: Paying Early

Suppose you borrowed money for 1 year and luckily you got money after 6 months, and you want to pay your loan immediately.  Your loan company might only charge you 50% such as shown in Figure 2.

Figure 2 – Computation of Interest of 1.00 peso compounded semiannually at a rate of 100% a year.

Scenario 2: Re-borrowing Money

Another scenario is to borrow the money for six months and re-borrow it again for another six months without paying the first loan. Note that this is the same as failing to pay a six-month loan for a year.  The question is, after borrowing 1 peso for six months with an interest of 50% the first six months and another 50% in the second six months, do you think your loan company will let you pay Php 2.00 for 1 year? Well – lucky you are if they do.

Table 1 – Computation of 1 peso loan compounded semi-annually at an annual rate of 100% interest.

Loan interests do not work that way. That is because from scenario 1, after 6 months, the amount that you have to pay the company is Php 1.50. Hence, if you re-borrow the money without paying the principal – or you failed to pay it for another six months – the principal amount during your second loan will not be Php 1.00 but Php 1.50.  The computation of this scenario is shown in the table in Table 1 and is called compound interest. That is applying the interest rate not only to the principal amount (which Php 1.00 in the first six months), but also including the interest (which is Php 0.50 in the first six months).

If we have a fixed rate, say 100% (or 1 in decimal equivalent), then we have to divide it into the number of times that we are going to compound our interest in one year. For instance, applying a 100% interest to a one-year loan compounded monthly will require us to divide 100% by 12 which is 8.5% per month or 0.085 in decimal equivalent. Table 2 shows the computation of this scenario. In January, the principal is only Php 1.00 and after applying the interest, the amount payable is 1.085. That means, if you want to pay at the end your January, you have to pay 1.085 or 1.09 pesos. This becomes the principal amount in February. If we multiply 1.085 by 0.085, our interest in February is 0.092. If we add this to the principal amount in February, which is 1.085, then the amount payable by the end of February is 1.177 peso or 1.18 pesos.

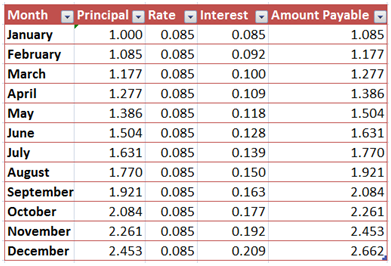
Table 2 – Computation of Interests of a 1-peso loan compounded monthly at a 100% annual interest rate.

This process is repeated until December.  As shown in the table, by the end of December, 2.66 is the amount payable for the 1-peso loan for 1 year with 100% interest compounded monthly.

Generalization

Putting the principal and interest in table in Figure 3 into computation, we have the following.

Figure 3 – Computation of Amount Payables given the number of compounds per year.

Looking at Figure 3,  in the January row of Table 2, we have a principal of 1 and an interest rate of 0.085 = 1/12. Thus, using the pattern shown in Figure 3, in general, if we have 1 as principal, 100% as annual interest, and n as the number of times we are going to compound the interest in a year, then the amount payable after a year can be computed by the formula (1 + \frac{1}{n})^n. Several questions may arise following the discussion above:

  1. What happens as the number of compound is getting larger and larger? What happens if we compound per day, per hour, per minute and per second?
  2. What happens if we divide 1 (that is, 100%) into a very large number? Will the amount payable reach a very large number? Will amount payable reach infinity?

Using 1-peso as principal and 1 (or 100%) as interest per year, the table below shows the amount payable given the number of times the interest is compounded in a year. As we can see, compounding daily gives approximately 2.714 pesos and compounding every second 2.718, only a difference of 0.004.  It is evident that as the number of compounds of year increases, the smaller the increase in amount payable per year.

Does that mean that the amount payable is approaching a particular number?

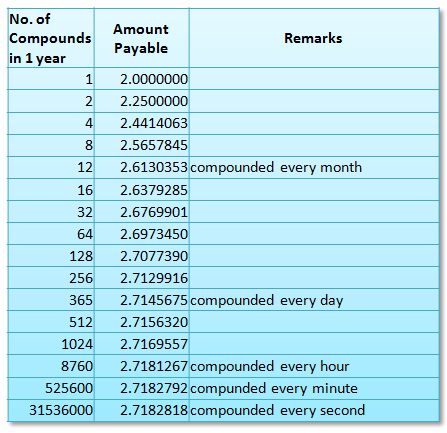
Table 3 – Computation of Amount Payables given the number of compounds per year.

Also, from the table, it seems that as the number of compounds increases, the amount payable is approaching 2.7182818. In fact, raising the number of compounds per year to 1 billion gives us  2.7182820, an increase of 0.02. This means, that this number has a limit as we increase the number of compounds per year.

The number that is the limit of the expression (1 + \frac{1}{n})^n is called e in mathematics and is approximately equal to 2.718282. That is \lim_{n \to \infty} (1 + \frac{1}{n})^n = e. The irrational constant e is a very important number in mathematics just like \pi. It is be seen in many mathematical fields. In future posts, we are going to discuss why e is so important and where e usually appears.

Leave a comment , , , , , , , , , , ,

A Closer Look at the Midpoint Formula

High School Algebra, High School Geometry, High School Mathematics

Introduction

If we want to find the midpoint of segment CD in Figure 1, where the coordinates of points C and D are (-2,5) and (-2,1), it is clear that the length of CD is 5 - 1 = 4 units.  To determine the midpoint of CD, we want to get the coordinates of the point which is 2 units away from both points C and D.  Hence, we have to divide 5 - 1 = 4 by 2, and add the result to 1 or subtract the result from 5.  Summarizing, the expression that would describe the value of the y-coordinate of the midpoint would be \displaystyle\frac{(5 - 1)}{2} + 1 or  5 - \displaystyle\frac{(5 - 1)}{2}. This means that the midpoint of CD is (0,2).

If we want to get the midpoint of AB, using the same reasoning above, the expression that would describe the x-coordinate of the midpoint would be \displaystyle\frac{(6 - 3)}{2} + 3 or 6 - \displaystyle\frac{(6 - 3)}{2}. This means that the midpoint of AB is (1.5,0).

Figure 1 – Horizontal line AB and vertical line CD in the coordinate plane.

Generalizing our observation above, if we have a vertical segment with their endpoints having coordinates (a, y_1) and (a,y_2) (see Figure 2), we can get its midpoint  using the following formula \displaystyle\frac{y_2 - y_1}{2} + y_1  or y_2 - \displaystyle\frac{y_2 - y_1}{2} + y_1

Figure 2 – Generalized coordinates of a vertical and a horizontal line.

Simplifying, both the expressions above result to \displaystyle\frac{y_2 + y_1}{2}. Similarly, for a horizontal segment with endpoints having coordinates (x_1, b) and (x_2, b) can be computed by the expression \displaystyle\frac{x_1 + x_2}{2}.

Midpoint of a Slanting Segment

The preceding derivations are only valid for vertical and horizontal segments. In Figure 3, segment AB is neither horizontal nor vertical. To investigate the midpoint of AB, we draw vertical segment PQ coinciding with the y-axis with endpoints having y-coordinates the same as those of the y-coordinates of segment AB (see Figure 3). We also draw a horizontal line RS coinciding the x-axis with endpoints having  x-coordinates the same as those of the x-coordinates of segment AB. Looking at Figure 3, it is clear that the coordinates of the midpoint of the PQ is (0,3).

If we draw a horizontal line from (0,3) towards segment AB (see yellow dashed segment), and draw a vertical line from the intersection M to segment RS, it seems that the intersection of the yellow dashed line and segment RS is (3.5,0) which is the midpoint of RS. From here, it is tempting to ask the following question:

“If the midpoint of PQ is (0,3) and the midpoint of RS is (3.5,0), is the midpoint of AB, (3.5,3)?

Figure 3 – A non-horizontal segment AB with midpoint M.

Generalizing the questions above, we might want to ask “If the midpoint the point with coordinates A (x_1,y_1) and B (x_2, y_2) equal to (\displaystyle\frac {x_1 + x_2}{2}, \displaystyle\frac{y_1 + y_2}{2})?”

If we extend the QA and the horizontal yellow dashed line to the right, we can from two right triangles as shown in Figure 4. From the statements above, we want to show that point M is the midpoint of AB.

To show that M is the midpoint of AB, it is sufficient to show that AM is congruent to MB.  This leads us to Figure 5, where we label the right angles of the two triangles T and U. We will now show that triangle AUM is congruent to triangle MTB. If so, then we can show that AM is congruent to MB since they are the corresponding sides of the given triangles.

Proof that AUM is congruent to MTB

Since PB and MT are horizontal segments, we can consider AB as a transversal of parallel segments PB and the segment containing MT.  It follows that angle TBM and angle UMA are congruent because they are corresponding angles. It is also clear that BT is congruent to MU, and angle T is congruent to angle U since they are both right angles. Therefore, by the ASA congruence theorem, AUM is congruent to MTB.  (For an explanation of parallel lines and transversals, click here).

Since corresponding parts of congruent triangles are congruent, AM is congruent to MB. Hence, M is the midpoint of AB.

Figure 5 – The triangle produced by extending the horizontal lines passing through the three points.

Note that our proof did not talk about coordinates, but the general case.  That is, if the coordinates of A are ( x_1, x_2) and the coordinates of B are (y_1, y_2), the coordinates of M is equal to (\displaystyle\frac{x_1 + x_2}{2},\displaystyle\frac{y_1 +yx_2}{2} ).

Delving Deeper

There are also other ways to show that the midpoint of AB is M.  ( x_1,y_1) and ( x_2,y_2) lies on  the midpoint formula. The details of the solutions are left to the reader as an exercise.

  • From Figure 3, draw two right triangles with hypotenuse AM and hypotenuse AB and show that AM is half of AB.
  • Using the distance formula, show that the distance between point A and point M is the same as the distance between point M and point B.
  • Show that AM and MB has the same slope.
  • Get the equation of the line containing AB, and substitute the coordinates of M to the equation of line AB.
3 comments , , , , , , , , , , , , , ,

How to use the summation symbol

High School Algebra, High School Mathematics

If we want to add the expression x_1,x_2 all the way up to x_{10}, it is quite cumbersome to write x_1 +x_2 + x_3 + x_4 + x_5 + x_6 + x_7 + x_8 +x_9 +x_{10}. Mathematical notations permit us to shorten such addition using the \cdots symbol to denote “all the way up to” or “all the way down to”. Using the this symbol, the expression above can be written as x_1 + x_2 + \cdots + x_{10}.

There is, however, a more compact way of writing sums. We can use the Greek letter \Sigma as shown below.

Figure 1 – The Sigma Notation

In the figure above, a is the first index, and letter b is the last index.   The variable(s) are the letters or the numbers that appear constantly in all terms. In the expression

x_1 + x_2 + x_3 + x_4 + x_5 + x_6 + x_7 + x_8 + x_9 + x_{10}

1 is the first index, 10 is the last index and x is the variable. We use the letter i as our index variable, or the variable that will hold the changing quantities.  Hence, if we are going to use the sigma or the summation notation for the expression x_1 + x_2 + x_3 + x_4 + x_5 + x_6 + x_7 + x_8 + x_9 + x_{10}, we have

\displaystyle\sum_{i=1}^{10} x_i

Some of the examples are shown below.  Observe the colors of the indices and the variables, to familiarize yourself how the summation symbol works.

Figure 2 – Examples of Summation Notation

In using the summation symbol, take note of the following:

  • An index variable is just a “dummy” variable. It means that you can use a different index variable without changing the value of the sum. The sum \displaystyle\sum_{i=1}^{10} a_i is the same as \displaystyle\sum_{j=1}^{10} a_j and is the same as \displaystyle\sum_{k=1}^{10} a_k.
  • The indices are the natural numbers 1, 2, 3, \cdots and so on.
  • The last index is always greater than the first index.
  • A variable without an index most of the time represent an infinite sum or a sum from 1 through n

More Examples

1. (a - 1) + (a^2 - 2) + (a^3 - 3) + (a^4 -4) \displaystyle\sum_{i=1}^{4} (a^i - i)
2. 3p_5 + 3p_6 + 3p_7 + 3p_8 \displaystyle\sum_{j=5}^{8} 3p_j
3. 5 + 5 + 5 + 5 + 5 + 5 + 5 \displaystyle\sum_{k=1}^{7} 5
4. 1 + 2 + 3 + \cdots + 99 + 100 \displaystyle\sum_{m=1}^{100} m
5. (a_3 + b_3) + (a_4 + b_4) +(a_5 + b_5) \displaystyle\sum_{n=3}^{5} (a_n + b_n)

Properties of the Summation Symbol

1.) The expression (x_1 + x_2 + x_3 + x_4) + (x_5 + x_6 + x_7 + x_8 + x_9 + x_{10}) equals (x_1 + x_2 + x_3 + x_4 + x_5 + x_6 + x_7 + x_8 + x_9 + x_{10}) which means that \displaystyle\sum_{i=1}^{4} x_i + \displaystyle\sum_{j=5}^{10} x_j = \displaystyle\sum_{i=1}^{10} x_i . In general, \displaystyle\sum_{i=1}^{m} x_i + \displaystyle\sum_{j=m+1}^{n} x_j = \displaystyle\sum_{i=1}^{n} x_i.

2.)The expression (x_1 + x_2 + x_3 + x_4) + (y_1 + y_2 + y_3 + y_4) = \displaystyle\sum_{i=1}^{4} x_i + \displaystyle\sum_{j=1}^{4} y_j. Regrouping the expression, we have  (x_1 + y_1) + (x_2 + y_2) + (x_3 + y_3) + (x_4 + y_4) = \displaystyle\sum_{i=1}^{4} (x_i + y_i). This means that \displaystyle\sum_{i=1}^{4} x_i + \displaystyle\sum_{i=j}^{4} y_j = \displaystyle\sum_{i=1}^{4} (x_i + y_i) Generalizing, we have \displaystyle\sum_{i=1}^{n} x_i \pm \displaystyle\sum_{j=1}^{n} y_j = \displaystyle\sum_{i=1}^{n} (x_i \pm y_i).

3.) The expression c + c + c + \cdots + c (k of them) = \displaystyle\sum_{i=1}^{k} c. But c + c + c + \cdots + c = c( 1 + 1 + 1 + \cdots + 1) (k of them) = kc. Therefore, \displaystyle\sum_{i=1}^{k} c = kc.

4.) The expression 2x_1 + 2x_2 + 2x_3 + 2x_4 = \displaystyle\sum_{i=1}^{4} 2x_i. But 2x_1 + 2x_2 + 2x_3 + 2x_4 = 2(x_1 + x_2 + x_3 + x_4) = 2 \displaystyle\sum_{i=1}^{4} x_i.  In general, \displaystyle\sum_{i=1}^{k} cx_i = c \displaystyle\sum_{i=1}^{k} x_i.

Leave a comment , , , , , ,
1 … 27 28 29 30 31