A Calculus Primer Part 3
This is the third part and the conclusion to the Mathematics and Multimedia’s Calculus Primer Series. The first part can be read here and the second part can be read here.
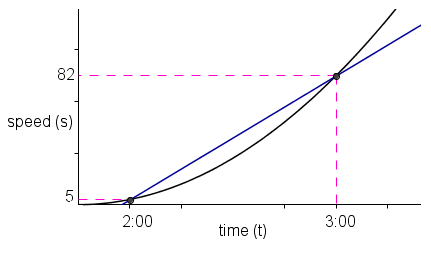
In the previous part of this series, we have discussed how mathematicians of the ancient times found clever ways to find the area of regions bounded by curves. We used this knowledge to generalize a way to solve the distance traveled by an accelerating car. In this post, we continue with the discussion of the second problem: How do we find the acceleration of the car at a particular instance?
Recall that in the problem, at 2 o’clock, the speed of the car is 5 kilometers per hour and at 3 o’clock, its speed is 120 kilometers per hour. So, the acceleration is 77 km/hr/hr. » Read more