Category: Geometer's Sketchpad

Geometer’s Sketchpad Essentials Series

Geometer's Sketchpad

Before I became a GeoGebra user, I had been a user of Geometer’s Sketchpad (GSP version 4.07) for quite some time. Although I am a great fan of GeoGebra, GSP requires more mathematical maturity to use, and in several aspects, has also its advantages. Sometimes, I am tempted to write a comparison between the two software, but I fear that I might be biased because I haven’t been using GSP very much nowadays.

This tutorial series will discuss the basics of GSP,  and is parallel to the GeoGebra Essentials Series.   The future topics  are as follows: » Read more

Leave a comment , ,

Geometer’s Sketchpad Tutorial 4 – Constructing a Square

Geometer's Sketchpad, Software Tutorials

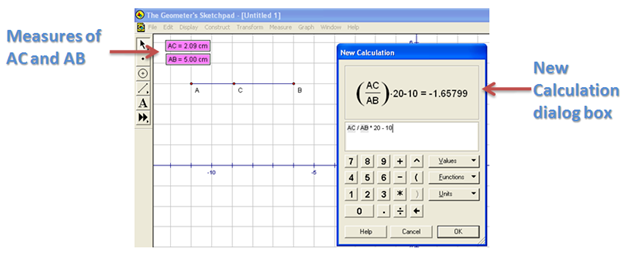
In this tutorial, we will use the Geometer’s Sketchpad version to mimic the compass and straightedge construction tool we use in elementary geometry.

The idea in constructing a square is to use the radii of congruent circles. Before beginning the construction, see Figure 3 so that you will have an idea of what we are going to do. In Figure 4, segment AB is created, then two congruent circles, one with center A and passing through B, the other with center B passing through point A.  The intersections of the circle and the line (points C and D) are the third and the fourth vertex of the square.

Step-by-Step Constructions

1.) Click the straightedge tool and select Segment Tool, then click two different locations on the drawing area.
2.) Click the Selection Arrow Tool, click on a blank space in the drawing pad to deselect the segment. To show the label of the two points, select the two points, click the Display menu, then click Show labels. Notice that GSP names the points alphabetically – the first A and the other B.

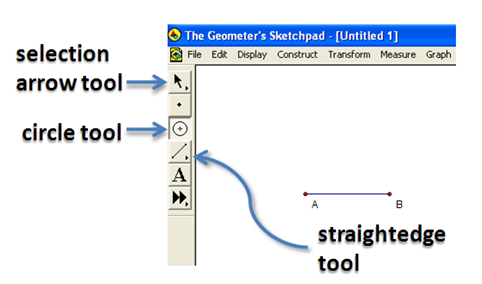
Figure 1 – Segment AB and the GSP toolbar.

3.) To construct two lines perpendicular to segment AB, one passing through A and the other through B, click the segment (be sure that the two points are also selected), click the Construct menu, then click Perpendicular lines. Your construction should look like the one shown in Figure 1.

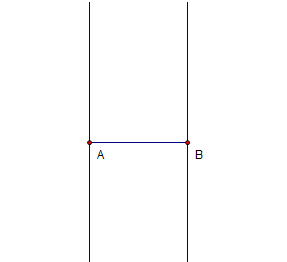
Figure 2 – Segment AB with lines perpendicular to it passing through its endpoints.

4.) Next, we will construct a circle with center B passing through A. To do this, click the circle tool, click point B and then click point A.
5.) We will now intersect the circle and the line passing through point B. To do this, click the Point tool, hover over the intersection of the circle and the line through B, wait for the two objects to change their color to cyan, then click their intersection.
6.) To display the label of the third point, with the third point selected, click the Display menu, then click Show label.

Figure 3 – Point C is the intersection of the circle and the line passing through B.

7.) Next, create a circle with center A and passing through B. Refer to step 4.
8.) Intersect the line passing through A and the circle with center A to construct point D.
9.) Show the label of the fourth point.

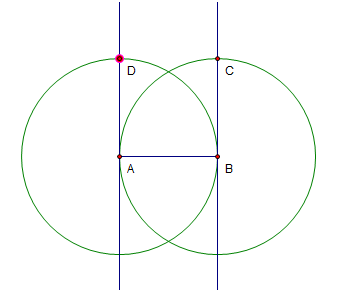
Figure 4 – ABCD is going to be the vertices of the squares.

10.) Next, we will hide the circles and the lines. Click the Selection Arrow tool, click the two circles and the two lines, then click Hide Path Objects.
11.) To form the square, use the Segment tool to connect the vertices of the square.
12.) Move the vertices of the square and observe what happens.  Explain why your observation is such.

Leave a comment , ,

Geometer’s Sketchpad Tutorial 3: Graphs and Sliders

Geometer's Sketchpad, Software Tutorials

In this tutorial, we are going to use Geometer’s Sketchpad to explore the graph of the function y = mx + b where m and b are real numbers. First, we are going to type each equation manually, but later, we are going to use sliders to see the relationship between the parameters m and b and the appearance of the graph.

Steps Graphing Equations

  1. Open Geometer’s Sketchpad.
  2. Click the Graph menu from the menu bar and click Define Coordinate System from the  list.
  3. To graph the function y = 2x, click the Graph menu, then click Plot New Function to display the New Function dialog box.
  4. In the New Function dialog box, type 2x, then click the OK button.

Figure 1 – The New Function dialog box.

Using steps 1 through 4, graph the following functions and observe how the value of m affects the graph of y = mx

  1. y = 3x
  2. y = 4x
  3. y = 5x
  4. y = 10 x
  5. y = – 2x
  6. y = – 4x
  7. y = -6x
  8. y = – 10x

Graph the following functions and observe how b affects the graph of the function y = mx + b.

  1. y = 2x + 3
  2. y = 2x + 1
  3. y = 2x + 5
  4. y = 2x – 1
  5. y = 2x – 4
  6. f. y = 2x – 10

Creating a Slider

There is a better way to explore the relationship of the parameters of functions and their graphs. Instead of typing each equation, we can use the sliders to assign values to parameters like m and b. A slider is a visual representation of a number. For instance, if you have a slider m with domain -10 through 10, then moving the slider rightward will increase the value of m. The slider that we will create here is very similar to Graphs and Sliders 1 and Graphs and Sliders 2 posts in the GeoGebra Tutorial Series.

The construction of slider in Geometer’s Sketchpad is somewhat different compared to the slider in GeoGebra. We will use the idea of ratio in creating a slider here.  To create a slider, we will construct segment AB, and construct point C on AB. We will divide the measure of AC by the measure of AB,then multiply it to 20. This means that our minimum value is 0 and our  maximum number is 20. To facilitate negative values, we will subtract 10 from result of our computation. This means that our minimum value is 0 – 10 = -10 and our maximum value is 20 – 10 = 10.

If you want to extend the domain of your slider, you just multiply the quotient of AC and AB by your desired number and subtract half of that desired number from the product.

Figure 2 – The slider control consisting of point C on segment AB.

Steps in Constructing a Slider

  1. Open Geometer’s Sketchpad.
  2. To show the coordinate axes, click the Graph menu from the menu bar and click Define Coordinate System from the drop-down list.
  3. To construct our slider, click the Segment tool from the toolbox, and construct a horizontal segment on the drawing area.
  4. To display the label of the two points, select the two points, click the Display menu from the menu bar and click Show Labels from the list.
  5. To construct point C on AB, click the Point tool and click segment AB (not the points).
  6. Display the label of point C, by right clicking it and choosing Show label from the pop-up menu.
  7. For our computation of the value of m, we first measure the value of AC and AB. To measure AC, select points A and C (be sure that only the two points are selected), click the Measure menu and click Distance from the list.
  8. To measure AB, select points A and B, then click the Measure menu and click Distance from the list.

    9. Figure 3 – The Measure-Distance command displays the distance between two points.

  9. To find the value of m, we divide AC by AB, multiply the result to 20 and the subtract 10. To do this, click the Measure menu and click Calculate from the list.
  10. Click the text on the drawing area displaying the measure of AC, click the ÷ button from the New Calculation dialog box, click the label displaying the measure of AB, click * from the New Calculation dialog box, then type 20-10, then click the OK button on the dialog box when finished.  This will be our value of m.

    11. Figure 4 – The New Calculation dialog box.

  11. Move point C and observe what happens to the value of m. If you want to Edit your calculation, just click the Arrow tool, right click the the value of m, then click Edit Calculation.

    12. Figure 5 – The pop-up menu that appears when you right click the value of m.

  12. To graph y = mx, click the Graph menu, then click Plot New Function to display the Plot New Function dialog box.
  13. While the Plot New Function box is displayed, click the label containing the value of m, click the * button, click the x (or type x), then click the OK button. If you have followed the steps correcty, the graph of y = mx should appear in your coordinate system.
  14. Hide points A and B and the labels containing the values of AB and AC by clicking the Display menu and click Hide Objects.
  15. Move point C. What do you observe? What relationship can you conclude between the value of m and the appearance of the graph of the function?

Exercise:

  1. Construct another slider for the value of b.
  2. Construct a graph that will display the value of f(x) = mx + b.
  3. Describe the effect of b in the graph of the function f(x) = mx + b.
9 comments , , , , , , , ,
1 2 3 4 5