Tag: paper folding

Using Paper Folding to Introduce the Notion of Proof

High School Geometry, High School Mathematics

Two years ago, I worked as part-time geometry instructor in a technical school near our university.  Most of the students in that school were quite clueless about the notion of proofs, so I tried to find ways to introduce proofs in an intuitive manner.

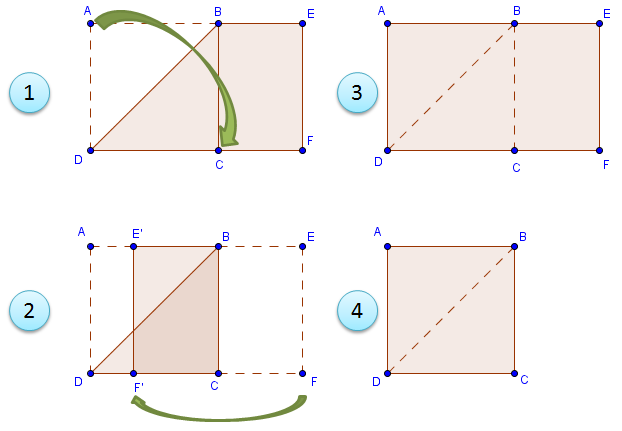
One lesson I developed was on proving that a quadrilateral formed from paper folding is a square.  I let the students create a square from a piece of bond paper without using any measuring instrument; only folding and cutting were allowed.

proof

As expected, most of the students used the method shown in the figure above. For the sake of discussion, we label the corners and critical points of the bond paper.  Most of the students constructed the square using the following steps (see figure): » Read more

3 comments , ,

Paper Folding: The proof of the cube root applet

High School Geometry

Last week, we have discussed the second part of our Paper Folding series, a fold that extracts the cube root of any number.   In this post, we are going to discuss its proof, but before that, let’s recall how to do the paper fold.

Paper Folding Instructions 

  1. Get a rectangular piece of paper and fold it in the middle, horizontally and vertically, and let the creases (see green segments in the applet) represent the coordinate axes.
  2. Let M denote (0,1) and let R denote (-r,0).
  3. Make a single fold that places M on y = -1 and R on x=r.
  4. The x-intercept of the fold is \sqrt[3]{r}.
The GeoGebra applet below visualizes the fold. Drag points P and Q to satisfy the conditions above. Note that you can also move point R.  » Read more
One comment , , ,
1 2 3