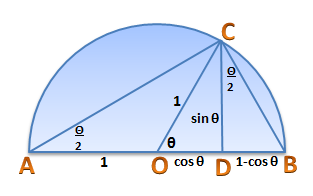
proof without words Archives - Page 2 of 2

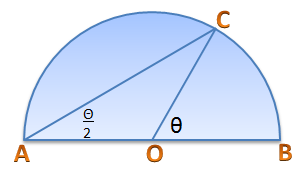
Proof of the Sum of Square Numbers

May 27, 2012 GB High School Mathematics, High School Number Theory

In the first part of this series, we have counted the number of squares on a chessboard, and we have discovered that it is equal to the sum of the squares of the first 8 positive integers. The numbers $1^2$ , $2^2$ , $3^2$ and so on are called square numbers.

This method can be generalized to compute for the number of squares on larger square boards. If the measure of a board is $n \times n$ , then the number of squares on it is » Read more

5 comments google sketchup, number of squares on chessboards, proof sum of square numbers, proof without words, sum of square numbers

The Proof of the Tangent Half-Angle Formula

May 3, 2012 GB High School Mathematics, High School Trigonometry, Problem Solving and Proofs

In this post, we prove the following trigonometric identity:

$\displaystyle \tan \frac{\theta}{2} = \frac{\sin\theta}{1 + \cos \theta} = \frac{1 - \cos \theta}{\sin \theta}$ .

Proof

Consider a semi-circle with “center” $O$ and diameter $AB$ and radius equal to 1 unit as shown below. If we let $\angle BOC =\theta$ , then by the Inscribed Angle Theorem, $\angle CAB = \frac{\theta}{2}$ .

Draw $CD$ perpendicular to $OB$ as shown in the second figure. We can compute for the sine and cosine of $\theta$ which equal to the lengths of $CD$ and $OD$ , respectively. In effect, $BD = 1 - \cos \theta$ and $AD = 1 + \cos \theta$ . » Read more

2 comments half angle formula, half angle formula identity, half angle formula proof, inscribed angle theorem, proof without words, trigonometric identities, trigonometric identity

Mathematics and Multimedia Blog Carnival #3

September 13, 2010 GB Blog Carnival, High School Mathematics

Welcome the third edition of the Mathematics and Multimedia blog Carnival. This will be the last edition that I will be hosting this year. The fourth edition will be hosted by Wild About Math!.

Before we begin, let’s have some interesting trivia about the number three. » Read more

14 comments GeoGebra, graphing linear model, ICT-based homeworks, math 2.0, mean, median and mode, movie showing in class, multiplication facts, multiplying algebraic expressions, natural math, online manipulative, proof without words, pythagorean theorem, radian measure, square and square roots, virtual origami, wild about math, Wolfram Alpha

« 1 2