Tag: real numbers

Real Numbers: A Summary

High School Mathematics

For the past two years, we have talked a lot about real numbers.  We have talked about integers and its operations (addition, subtraction, multiplication, and division), we have discussed about rational and irrational numbers, and we have talked about their properties, structure, and wonders. In this post, we are going to summarize what we have learned about them.

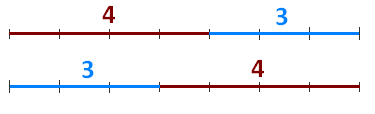
Figure 1 - The Number Line

The set of real numbers is the collection of all rational and irrational numbers. By convention, real numbers are represented by a line infinitely long where the positive real numbers are situated at the right hand side of 0, while the negative are at the left hand side. It is also important to note that for each point on the number line, there exists a corresponding real number equivalent to it, and for each real number, there is a corresponding point on the line that represents it. » Read more

9 comments , , , , , , ,

Operations on Integers – Addition

Elementary School Mathematics, High School Algebra, High School Mathematics

Introduction

The set of integers is composed of the negative integers, zero, and the positive integers.  The integers can be visualized using the number line (see first figure), a horizontal line, where, by convention (agreed upon by mathematicians), the negative numbers are located at the left of zero, and the positive integers at the right of 0. In the number line, the number a is greater than the number b if a is at the right of b. Therefore, -2 is greater than -3, -1 is less than 1, 0 is greater than -4.

As shown in the figure above, each integer has a specific location (coordinate) on the number line. Aside from being a coordinate on the number line, each integer can also be considered as movement from 0. For example, +2 means moving 2 units to the right of 0, while -3 is moving 3 units to the left of 0.

» Read more

7 comments , , , , , , , , , ,

The Geometry of Commutativity

High School Algebra, High School Mathematics

One of the elementary observations about real numbers is that if we add the two numbers, regarding of the order, their sum is unique.  We know that 4 + 3 = 3 + 4. This property is also the same when we multiply. If we have two numbers, regarding of the order, their product is also unique. For example, 6 x 3 = 3 x 6.

In general if we have real numbers a and b, we have a + b is always equal to b + a. Also, if we have real numbers c and d, c x d is always equal to d x c. These are called the commutative property of addition and multiplication, two of the axioms of algebra.

Although axioms, as we have discussed, are statements that we accept without proof, some axioms can be explained intuitively.  In this post, we are going to discuss the two axioms mentioned above intuitively using geometric representations.

The geometry of a + b

One way of understanding why a + b is always equal to b + a is by representing the two numbers as lengths. For instance, we can represent the addition of integers above (4+3 = 3 + 4) as the sum of the lengths of two segments. In geometric representation, reversing the order of the numbers in the operation is just like rotating the segment 180 degrees about the center as shown below. Of course, rotating the segment  way will never change its length.

Now, since that we can substitute any positive numbers to a and b we are sure that the commutative property is true for all positive numbers. » Read more

3 comments , , , , , ,
1 2 3 4