Tag: triangle area

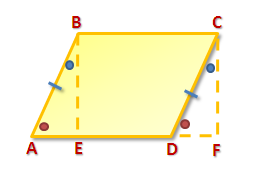
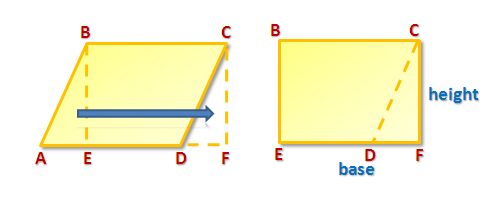
Linking sum of counting numbers to triangle area

High School Algebra, High School Geometry, High School Mathematics

We have discussed how Gauss was able to add the first 100 counting numbers, and we learned ways how to generalize his method.  In this post, we link his method in finding the area of triangles.

Adding the first few counting numbers is easy. However, as the numbers become larger, it becomes harder. According to an anecdote, Gauss at primary school was able to find a clever way of answering the question his teacher asked him:  What is the sum of all the numbers from 1 to 100?

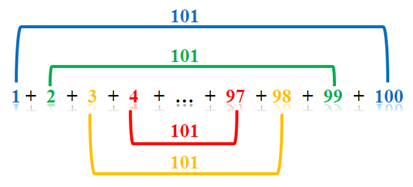Gauss method was to add the first and the last digit (1 and 100), the second and the second to the last digit (2 and 99), third and the third to the last digit (3 and 98), and found out that the sums were always 101. There are 50 pairs of numbers from 1 to 100 whose sum is 101. So,  the sum of all the numbers from 1 to 100 is (101)(50) = 5050. » Read more

One comment , , ,

Area Tutorial 5 – Area of a Trapezoid

Elementary School Geometry, Elementary School Mathematics, High School Geometry, High School Mathematics

In this tutorial, we are going to derive the area of a trapezoid. A trapezoid (sometimes called a trapezium) is a quadrilateral with exactly one pair of parallel sides. Trapezoid PQRS is shown below, with PQ parallel to RS.  We have learned that the area A of the trapezoid with bases b_1 and b_2 and altitude h is given by the formula A_{PQRS} = \displaystyle\frac{(b_1 + b_2)h}{2}.

Figure 1 - Trapezoid PQRS with PQ parallel to RS.

We are going to derive the area of a trapezoid in two ways: First by dividing into different sections and second by rotation.

Derivation 1: Area by Dividing into Regions

If we drop another line from Q, then we will have two altitudes namely PT and QU, which both have length h units.

Figure 2 - Trapezoid PQRS divided into two triangles and a rectangle.

From Figure 2, it is clear that Area of PQRS = Area of PST + Area of PQUT + Area of QRU. We have learned that the area of a triangle is the product of its base and altitude divided by 2, and the area of a rectangle is the product of its length and width. Hence, we can easily compute the area of PQRS. It is clear that A_{PQRS} = (ah/2) + b_1h + (ch/2).  Simplifying, we have  A = \displaystyle\frac{ah + 2b_1 + ch}{2}. Factoring we have, A_{PQRS} = (a + 2b_1 + c) \frac{h}{2} = [(a + b_1 + c) + b_1] \frac{h}{2}. But, a + b_1 + c is equal to b_2, the longer base of our trapezoid. Hence, A_{PQRS}= (b_1 + b_2) \frac{h}{2}.

Derivation 2: By Rotation

In the second derivation, we are going to duplicate the trapezoid and rotate it as shown below. It is evident that quadrilateral PS’P’S is a parallelogram (Why?). But we have learned that the area of the parallelogram is the product of its height and its base. Hence, A_{PS'P'S} = (b_1 + b_2)h.

Figure 3 - PQRS translated and rotated to form a parallelogram.

But the area of the trapezoid PQRS is half of the area of the parallelogram PS’P’S. Thus, A_{PQRS} = \displaystyle\frac{(b_1 + b_2)h}{2}.

Enjoy and Learn More

2 comments , , , ,

Area Tutorial 3 – Area of a Parallelogram

Elementary School Geometry, Elementary School Mathematics

In the previous area computation tutorials, we have learned how to compute the area of a rectangle and the area of a triangle.  In this tutorial, we are going to learn how to compute the area of a parallelogram.

In Figure 1, we have parallelogram ABCD with given base and the dashed segment as its height. If we drop down a vertical segment from point C and extend a horizontal segment from D to the right, we can form triangle CDF as shown in Figure 2.

Figure 1 – Parallelogram ABCD with a given base and height.

Now, angle ABE is congruent to angle DCF (Why?), AB is congruent to CD, and angle BAE is congruent to angle CDF. Hence, by ASA congruence postulate, triangle ABE is congruent to triangle DCF.

Figure 2 - ...

Since triangle BAE is congruent to triangle CDF, we can move ABE to coincide with DCF forming the rectangle in Figure 3. Click here to explore the translation using GeoGebra.

Figure 3 – Triangle ABE is translated and is superimposed to triangle CDF.

Since BCFE is a rectangle, its area therefore is the product of its base (length) and its height (width). We removed nothing from the parallelogram, therefore, the area of the parallelogram is the same as that of the area of the rectangle. Thus, the area of a parallelogram is the product of its base and its height.

Mr. Pilarski has almost a similar explanation but in video format.

Enjoy and Learn More

6 comments , , , , , ,