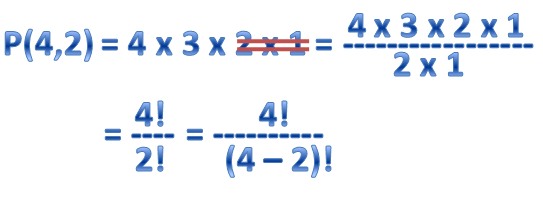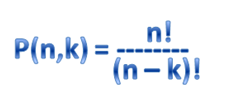Introduction to Permutations
Problem: In how many ways can Anna, Brenda and Connie stand in a single line for picture taking?
Intuitively, we can count the number of ways by listing. We can list randomly as shown below.
Anna, Brenda, Connie
Brenda, Connie, Anna
Connie, Anna, Brenda
and so on.
Q1: Do you think that listing randomly is a good idea? What are its advantages and its disadvantages?
Listing randomly can solve our problem, if there are only a few things, or in our case persons, to be arranged; however, we can do better than that. Learning mathematics has taught us to be organized, and has taught us to do things systematically. Besides, if there are many persons to be arranged, it is hard to keep track if we have listed all possible arrangements. For example, what if David joins the group? Try to list randomly and determine how many possible arrangements are there.
Q2: Before proceeding, can you think of a way to come up with an organized way to list all the possible arrangements?
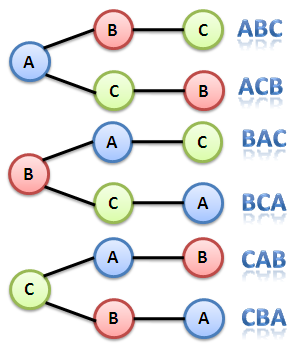
One possible strategy is to list in alphabetical order. Let us represent Anna, Brenda and Connie by the first letter of their names. If we choose A to occupy the leftmost position, then there are two possible choices for the middle position, namely B and C. That means have AB and AC as all possible arrangements if A is chosen to occupy the leftmost position. Now, in each of the cases, we only have one person left to occupy the rightmost position. This gives as ABC and ACB as all possible arrangements of the three girls if A were to occupy the leftmost position.
We can also use a tree diagram as shown in Figure 1. If we choose A to be the person in leftmost position, then the branches B and C mean our possible choices for the middle position. If we have chosen a person who will occupy the middle position, then we are left with only one person to occupy the rightmost position. Hence, if we choose A to occupy the first position, the only possible arrangements for picture taking are ABC and ACB.
But we know that we can also choose B or C as the person who will occupy the leftmost position. This means, that there are 3 possible choices for the first position, 2 possible choices for the second position and 1 possible choice for the third position (see Figure 1). Hence, there are 3 x 2 x 1 possible arrangements for 3 persons in a single line.
We will denote 3 x 2 x 1 as 3! (3 factorial). This implies that if we say 5!, we mean 5 x 4 x 3 x 2 x 1 = 120. In general, n! means n(n-1)(n-2)…(3)(2)(1). Note that the ellipsis symbol … denotes that there are numbers in the sequence that are not shown. For example, 100(99)(98)…(3)(2)(1), means the product of all integers from 100 all the way down to 1.
Q3: If David joins the group, how many possible arrangements are there?
You may want to solve this problem first before proceeding.
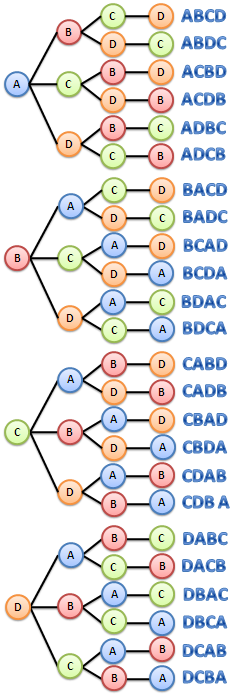
Looking at the tree diagram, there are four possible choices to occupy the leftmost position, 3 possible choices to occupy the second position, 2 possible choices to occupy the third position and 1 possible choice to occupy the rightmost position. Hence there are 4! = 4 x 3 x 2 x 1 = 24 possible arrangements.
By now, you would have realized that the number of arrangements or the number of permutations of n persons on a single line for picture taking is n!. We will denote it as P(n,n) orthe permutations of n objects taken n at a time. We sayn objects taken n at a time because we have the choice to choose numbers less than n to be arranged. For example, we can choose A and C from A, B, C and D . This means that we a permutation of 4 objects taken 2 at a time. In general, we describe this type of permutation as permutations of n objects taken k at a time and write P(n,k).
Let us see what happens to our computation with P(4,2). Since there are 4 possible choices for the first choice, and 3 choices for the second position, therefore, there are 4 x 3 possible permutations. This is the same as removing the smallest two factors by division. If we do this, we come up with the following computation:
If we list the elements of P(4,2), we have the following: AB, BA, AC, CA, AD, DA, BC, CB, BD, DB, CD, and DC. Indeed, we have 12 possible arrangements.
With our findings above, let us try to perform a few more computations and see if we can find a pattern.
Therefore, by looking at the pattern, we can conclude that the number of permutations of n things taken k at a time described by the formula
You may want to read Introduction to Combinations, the continuation of this post.