Category: High School Trigonometry

An Easy Way To Learn The Basic Trigonometric Identities

High School Mathematics, High School Trigonometry

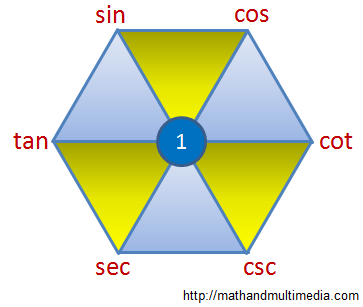
First learn the structure. Learn the positions of the six trigonometry functions. First comes the \sin function, underneath it comes the \cos function.

trigonometric identities

Then in the next column comes the \csc function, underneath it comes the \sec function. And in the last column comes the \cot function and underneath it comes the \tan function. Learning this position is important and just one time. The six trig functions are specially placed in the above given places, so as to serve our need.  » Read more

One comment , , , ,

The Trigonometric Ratio Hexagon

High School Mathematics, High School Trigonometry

I found a book this morning containing a hexagonal figure of trigonometric ratios.  It reminded me of the mnemonics I created when I was still in high school in order to remember the formulas during exams. Unlike in other countries, we were not allowed to have formula sheets during exams, so we have to memorize them all.

Trigonometric Ratio

In the figure, any trigonometric ratio is a product of its immediate neighbors. Therefore,  » Read more

One comment , , , ,

The Proof of the Tangent Half-Angle Formula

High School Mathematics, High School Trigonometry, Problem Solving and Proofs

In this post, we prove the following trigonometric identity:

\displaystyle \tan \frac{\theta}{2} = \frac{\sin\theta}{1 + \cos \theta} = \frac{1 - \cos \theta}{\sin \theta}.

Proof

Consider a semi-circle with “center” O and diameter AB and radius equal to 1 unit as shown below.  If we let \angle BOC =\theta, then by the Inscribed Angle Theorem, \angle CAB = \frac{\theta}{2}.

Draw CD perpendicular to OB as shown in the second figure. We can compute for the sine and cosine of \theta which equal to the lengths of CD and OD, respectively. In effect, BD = 1 - \cos \theta and AD = 1 + \cos \theta. » Read more

2 comments , , , , , ,
1 2