An Easy Way To Learn The Basic Trigonometric Identities

High School Mathematics, High School Trigonometry

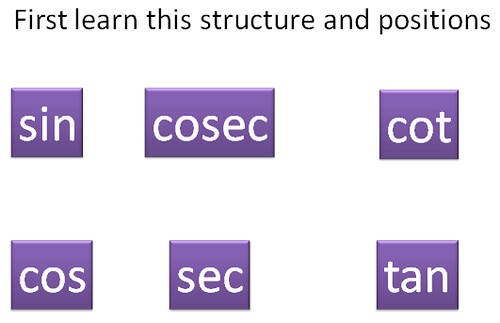
First learn the structure. Learn the positions of the six trigonometry functions. First comes the \sin function, underneath it comes the \cos function.

trigonometric identities

Then in the next column comes the \csc function, underneath it comes the \sec function. And in the last column comes the \cot function and underneath it comes the \tan function. Learning this position is important and just one time. The six trig functions are specially placed in the above given places, so as to serve our need. 

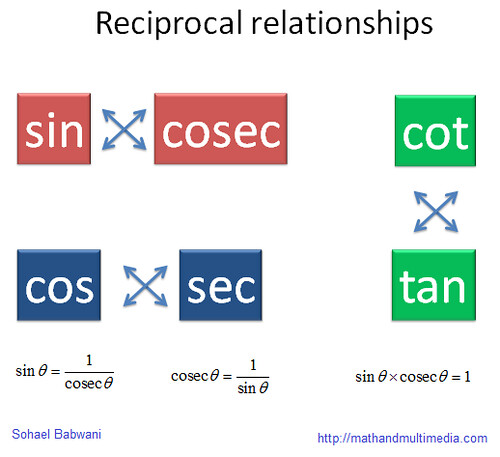
trigonometry-reciprocal-functions

Observe the second diagram. There is a cross placed in between \sin and \csc functions. This means that \sin and \csc are reciprocals of each other. That means

\sin \theta = \displaystyle\frac{1}{\csc \theta} and \csc \theta = \displaystyle \frac{1}{\sin \theta}

and  hence \csc \theta \times \sin \theta = 1 .

Similarly there is a cross in between \cos and \sec functions and hence they to are reciprocals of each other and their multiplication is 1. And the same with \tan and \cot functions.

Thus: \sin \theta = \displaystyle\frac{1}{\csc \theta} and \csc \theta = \displaystyle \frac{1}{\sin \theta} and  hence \csc \theta \times \sin \theta = 1 .

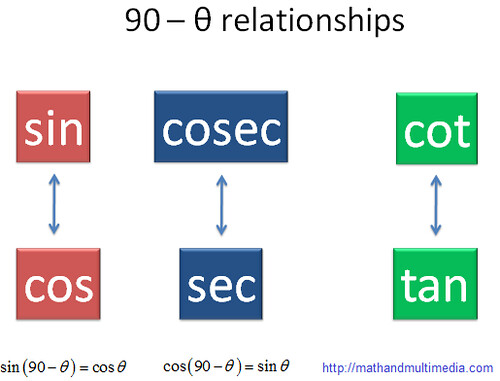
trigonometry-90minustheta

In the third diagram the functions which are connected with a line are complementary to each other and have 90 - \theta relationship. As we can see \sin and \cos are connected with a line and thus

\sin(90 - \theta) = \cos \theta; \cos(90 - \theta) = \sin \theta.

In the same way if you want to find 90 - \theta of any function, see which function is either above it or below it. In other words all the functions in the same column are complementary functions.

As you can see in the above diagram, all the functions have a square sign, because addition formulae are always expressed in squares. But remember the position does not change.

pythagorean-trigonometric-identities

Here \sin and \cos functions which lie in the same column are connected with the addition formula \sin^2 \theta + \cos^2 \theta = 1. See how wonderfully all the three addition formulae are shown in the diagram. You can also derive formulae like 1 - \cos^2 \theta = \sin^2 \theta from the above formula and hence no need to learn them separately. The above diagram also gives us other two addition formula 1 + \cot^2 \theta = \csc^2 \theta and  1 + \tan^2 \theta = \sec^2 \theta.

The best thing about the above diagrams is that you need to just remember the positions of the trig functions which function near them have the reciprocal relation, 90 - \theta functions and the addition functions. And also remember to write a square sign in case of addition function. Just for your easy understanding the interconnected functions are shown in same colour.

The Author

My name is Sohael Babwani from Mumbai, India. I give private tuitions to schoolchildren. I teach all subjects including Maths. In the year 2004, I had written an article “An Extended Approach to the Julian and the Gregorian Calendar.” This article was published in The Mathematical Gazette, London. I have made a blog/website http://www.babwani-congruence.blogspot.in/ explaining the same.

One comment , , , ,

Leave a Reply