Category: High School Number Theory

An Alternative Algorithm for Subtraction

High School Mathematics, High School Number Theory

In the previous posts, I have shared to you an alternative algorithm for multiplication and division. In this post, I am going to share with you a different algorithm for performing subtraction. This algorithm does not involve “borrowing” from a higher place value but subtracts individual digits. To illustrate this algorithm, let’s consider some examples.

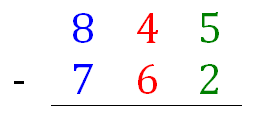
Example 1: 847 – 728

First, we separate the digits of the numbers as shown below.

Second, we subtract the corresponding digits.   » Read more

Leave a comment , ,

Euclidean Algorithm Explained for Elementary School

High School Mathematics, High School Number Theory

In number theory, the Euclidean algorithm is a method for getting the greatest common factor (GCF) or highest common factor (HCF) of two positive integers. It is usually used for larger numbers since prime factorization can be used to get the greatest common factor of small numbers. Many students are confused with this method, but if you look at it closely, even elementary students can actually do it.

Let us start with an example. Note that in the discussion below, we will use the terms dividend and divisor. In the division a ÷ b, a is the dividend and b is the divisor.  » Read more

Leave a comment , ,

The Mystery of the Four Consecutive Numbers in the Fibonacci Sequence

High School Mathematics, High School Number Theory

The Fibonacci Sequence

The Fibonacci sequence is the sequence of integers 0, 1, 1, 2, 3, 5, 8, 13, 21,…  or 1, 1, 2, 3, 5, 8, 13, 21, …  It is a sequence of numbers that starts with 0 (or 1) and  each number is the sum of the previous two. The sequence first appeared in Liber Abaci, a book written by Leonardo of Pisa, more popularly known as Fibonacci.

fibonacci sequence

The sequence appear in many branches as well as in many form. Take for instance the rectangle above. You can create  a rectangle whose sides are consecutive numbers of the Fibonacci Sequence. The Fibonacci Sequence also appears in the Pascal’s Triangle. » Read more

4 comments , , , ,
1 2 3 … 11