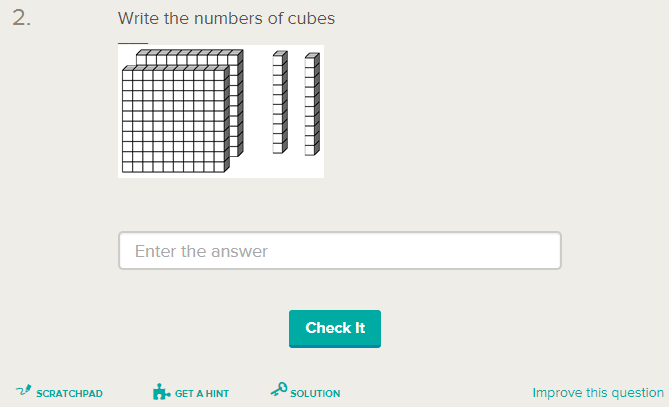
Mathematical Tasks: Number of Solutions and Answers
Different types of mathematical tasks let us tests the various skills of students. Close ended tasks let us test students basic knowledge of facts and procedures, while open-ended tasks lets us elicit various solutions answers. In the book Mathematical Thinking, Isoda and Katagiri classified mathematical tasks into three types:
Type 1: one solution, one answer
Type 2: many solutions, one answer
Type 3: many solutions, many answers
Examples of such problems are shown below. The first task is a Type 1 task, or a task with one solution and one answer. Students who have already learned how to calculate the area of rectangles can just use the formula to calculate the area of the rectangle. » Read more