Introduction to the DaMath Board Game Part 2
In the first part of this series, we have learned the basics of playing DaMath. We have learned the initial position of pieces on the board, how to move the pieces, how to capture the opponent’s piece, and how to score exchanges. In this post, we are going to learn how to capture multiple pieces.
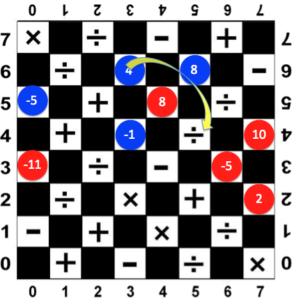
In DaMath, it is possible to capture multiple pieces. For example, in Figure 1, the Red Player placed 8 on (4,5). Now, the Blue Player is required to capture 8 using 4.
After capturing 8, it is now the Red Player’s turn to capture the Blue Player’s pieces as shown in Figure 2. Although capturing a piece is mandatory, capturing multiple pieces is optional. As shown, the Red Player is required to capture 4 using -5. However, he has also the option to capture -1 or 8. Note that capturing multiple pieces is considered as one move. Here are the possible cases. » Read more