Introduction to the DaMath Board Game Part 1
DaMath is a math board game coined from the word dama, a Filipino checker game, and mathematics. It was invented by Jesus Huenda, a high school teacher from Sorsogon, Philippines. It became very popular in the 1980s and until now played in many schools in the Philippines.
DaMath can be used to practice the four fundamental operations and also the order of operations. It has numerous variations, but in the tutorial below, we will discuss the Integers DaMath. Note that explaining this game is quite complicated, so I have divided the tutorial into three posts.
The DaMath Board
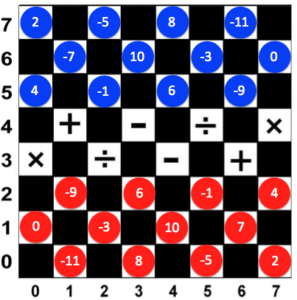
The board is composed of 64 squares in alternating black and white just like the chessboard. The four basic mathematical operations are written on white squares as shown in Figure 1. Each square is identified by a (column, row) notation. The top-left square, for example, is in column 0 and row 7, so it is denoted by (0,7).
DaMath is played by two opposing players. In this article, we will refer to them as the Blue Player and Red Player. The players take turns in moving the pieces.
The initial position of the pieces is shown in Figure 2. To start a DaMath game, a toss coin can be done to determine who will make the first move.
Moving the Pieces
The pieces are moved by sliding forward diagonally to a vacant adjoining square. This means that you can only move the pieces to white squares. All movements have to be diagonally forward; backward movements can only be made when capturing pieces or can be made by using a dama. A dama (like a Queen in chess) can also move backward and capture pieces backward. We will discuss the movements of damas in another post.
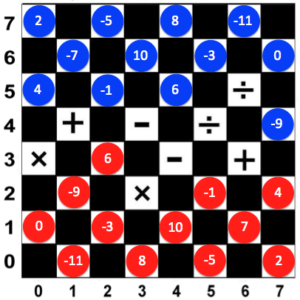
Suppose the Red Player moves first, he can move any of the four pieces in the front row one square forward diagonally. For instance, in Figure 3, the Red Player moved 6 to (2, 3) and then, the Blue Player moved -9 to (7,4).
We summarize the movements of the two players. Take note that the notation below is written on the scorecard during tournaments and school competitions.
First Move: Red 6 → (2,3); Blue -6 → (7,4).
Capturing the Pieces and Scoring
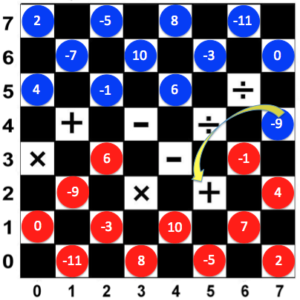
A piece captures an opposing piece by jumping over it diagonally and landing on the adjoining vacant square. Capturing is mandatory. In Figure 4, the Red Player moved -1 to (5, 3). The Blue Player is obliged to capture -1 using -9. He can do this by jumping -9 over -1 landing to (5,2) and removing -1 from the board. Here, -9 captured -1 and landed on a square with a + sign. Therefore, the score will be (-9) + (-1) = -10.
Blue Player’s Score: (-9) + (-1) = -10
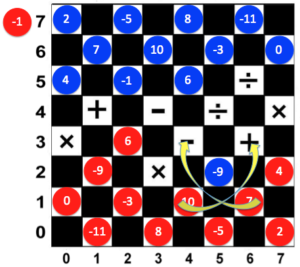
Figure 4 shows the position of the pieces after the Blue Player captured -1. It is now the Red Player’s turn to capture -9. As we can see, he can choose to use a 7 or a 10 to capture -9. However, using a 7 will yield a higher score. Using a 7 will result to 7 – (-9) = 16, while using a 10 will result to 10 + (-9) = 1.
Red Player’s Score: 7 – (-9) = 16
We can see that the Red Player is ahead of points. The players can continue playing and add the obtained scores each time a piece is captured. The player with the higher points at the end of the game wins the game.
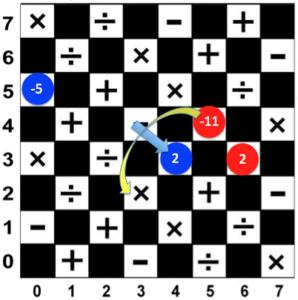
A piece can also capture backward. In the board position below, if it is the Blue Player’s turn to move, he can oblige the Red Player to capture 2 by moving 2 to the square on (4,5). The Red Player will have to capture 2 and -11 x 2 = -22 will be added to his score (i.e. Blue Player’s advantage).
A piece can also capture backward. In the board position below, if it is the Blue Player’s turn to move, he can oblige the Red Player to capture 2 by moving 2 to (4,5). The Red Player will have to capture 2 and -11 x 2 = -22 will be added to his score (i.e. Blue Player’s advantage).
In the second part of this post, we are going to discuss capturing multiple pieces.