Category: Elementary School Geometry

Eratosthenes and the Earth’s Circumference

Elementary School Geometry, Elementary School Mathematics

Eratosthenes was one of the most famous mathematicians in the early times. He was famous for his sieve – a strategy for finding prime numbers – but one of his greatest achievements was estimating the circumference of the earth. In this post, we learn how Eratosthenes used mathematics to solve the size of the earth. We  leave out some of the technical details (such that the assumption that the sun is so far away that its rays are almost parallel), since this post is for elementary school mathematics students.

How did he do it?

Eratosthenes knew that at noon in Syene, the sun casts no shadows. This can be tested using a sundial – a device used to tell the time using its shadow during the ancient time.

» Read more

4 comments , , , , ,

Is a square a rectangle?

Elementary School Geometry, Elementary School Mathematics, Questions and Quandaries

Note: This article is written for an elementary school students’ point of view.

_____

I have noticed that the topics I am discussing is getting deeper and harder, so let me break the spell by this very elementary question:

Are squares rectangles?

Before we answer that question, we must know first what a rectangle looks like, and we must also know its properties.  Many doors and windows, for example, are in a shape of a rectangle. We can observe that a rectangle has the following characteristics:

  1. It has four sides and four angles.
  2. The measure of its interior angles is 90 degrees.
  3. Opposite sides have the same lengths.
  4. Opposite sides are parallel.


For those who have already learned about the parallel postulate, you will probably agree that some of the observations above can be derived from the other properties, but we will leave it that way, for it is not that relevant in the following discussion. » Read more

4 comments , , ,

Area Tutorial 5 – Area of a Trapezoid

Elementary School Geometry, Elementary School Mathematics, High School Geometry, High School Mathematics

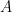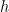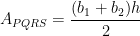In this tutorial, we are going to derive the area of a trapezoid. A trapezoid (sometimes called a trapezium) is a quadrilateral with exactly one pair of parallel sides. Trapezoid PQRS is shown below, with PQ parallel to RS.  We have learned that the area A of the trapezoid with bases b_1 and b_2 and altitude h is given by the formula A_{PQRS} = \displaystyle\frac{(b_1 + b_2)h}{2}.

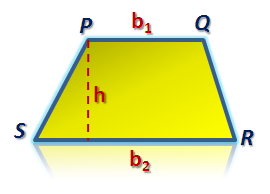
Figure 1 - Trapezoid PQRS with PQ parallel to RS.

We are going to derive the area of a trapezoid in two ways: First by dividing into different sections and second by rotation.

Derivation 1: Area by Dividing into Regions

If we drop another line from Q, then we will have two altitudes namely PT and QU, which both have length 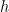h units.

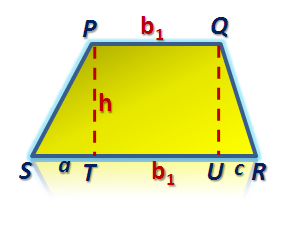
Figure 2 - Trapezoid PQRS divided into two triangles and a rectangle.

From Figure 2, it is clear that Area of PQRS = Area of PST + Area of PQUT + Area of QRU. We have learned that the area of a triangle is the product of its base and altitude divided by 2, and the area of a rectangle is the product of its length and width. Hence, we can easily compute the area of PQRS. It is clear that 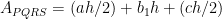A_{PQRS} = (ah/2) + b_1h + (ch/2).  Simplifying, we have  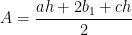A = \displaystyle\frac{ah + 2b_1 + ch}{2}. Factoring we have, A_{PQRS} = (a + 2b_1 + c) \frac{h}{2} = [(a + b_1 + c) + b_1] \frac{h}{2}. But, a + b_1 + c is equal to b_2, the longer base of our trapezoid. Hence, A_{PQRS}= (b_1 + b_2) \frac{h}{2}.

Derivation 2: By Rotation

In the second derivation, we are going to duplicate the trapezoid and rotate it as shown below. It is evident that quadrilateral PS’P’S is a parallelogram (Why?). But we have learned that the area of the parallelogram is the product of its height and its base. Hence, A_{PS'P'S} = (b_1 + b_2)h.

Figure 3 - PQRS translated and rotated to form a parallelogram.

But the area of the trapezoid PQRS is half of the area of the parallelogram PS’P’S. Thus, 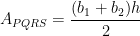A_{PQRS} = \displaystyle\frac{(b_1 + b_2)h}{2}.

Enjoy and Learn More

2 comments , , , ,
1 2 3