Area Tutorial 2: Area of a Triangle
In the previous area tutorial, we have learned that the area of a rectangle is equal to the product of its length and its width. For instance, the rectangle in Figure 1 has width 10 units and length 12 units, so its area is 120 square units. We have also learned in elementary school mathematics that the area of a triangle is half the product of its base length and its altitude.
Why is this so?

Figure 1 – Rectangle with length 12 units and width 10 units.
If we are going to relate the area of the triangle to the area of a rectangle given its length and width, then the easiest to compute is the area of a right triangle. In Figure 2, the rectangle is divided into two congruent triangles, which implies that the area of the triangle is half of the area of the rectangle. Also, the rectangle’s length became the triangle’s base and the rectangle’s width became the triangle’s altitude. Hence, it is clear that the area of the right triangle below is half the product of the length of its base and its altitude.
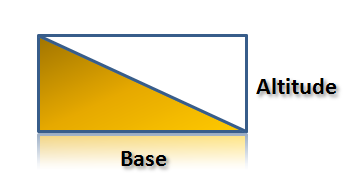
Figure 2 – The area of the right triangle is half the product of the base and the altitude of the rectangle.
The next question, however, is what if the triangle is not right? Does the formula still apply?
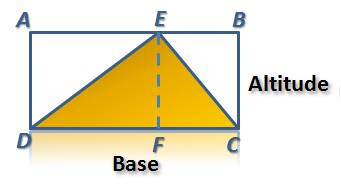
Figure 3 – The area of the non-right triangle above is still half the product of its base and its altitude.
In Figure 3, we have not changed the base and the altitude of the rectangle. If we draw a segment from the base to its opposite vertex (segment EF), then we form two smaller rectangles – rectangle AEFD and rectangle EFCB. From Figure 3, it is clear that the area of triangle EFD is half the area of rectangle AEFD. Also, the area of triangle EFC is half the area of rectangle EFCB. Thus, the area of triangle CDE is half the area of rectangle ABCD.
From the discussion above, we can conclude that if we can enclose a triangle with a rectangle with a given length (base) and width (altitude), then the area of that triangle is half the area of the enclosing rectangle. This is with the condition that the base of the triangle coincides with one of the sides of the rectangle, and the vertex opposite the base touches the side of the rectangle that is parallel to the base.
Does the formula work for all triangles?
The two cases above involve acute and right triangles, so what we have left is an obtuse triangle as shown below. As we can see, the vertex opposite the base is not touching the side of the rectangle that is parallel to the base.
One strategy in enclosing a triangle with a rectangle is to draw an altitude such that the altitude is inside the rectangle. In Figure 4, we cannot draw an altitude (perpendicular to the ground) inside the rectangle, so we will not be able to compute its area.
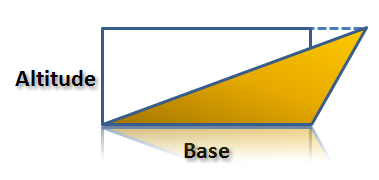
Figure 4 – An example of an obtuse triangle that cannot be enclosed by a rectangle using a particular side.
The remedy is shown in Figure 5. We change the base and change the altitude. In this case, the area of the triangle is half of the enclosing rectangle. This is true, since the condition above states that the length and width of the rectangle are given.
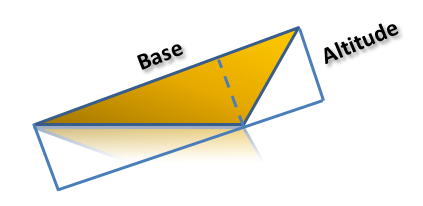
Figure 5 - Getting the area of a triangle by changing the base.
Delving Deeper
Playfair’s axiom guarantees that we can enclose any triangle with a rectangle, because given a line (base of a triangle) and a point (opposite vertex), we can always draw a unique line parallel to the base and passing through that vertex. To construct an enclosing rectangle, we can also draw two lines perpendicular to the base and passing through the other two vertices.
Enjoy and Learn More
- Area Tutorial 3 – Area of a Parallelogram
- Area Tutorial 4 – Area of a Circle
- Area Tutorial 5 – Area of a Trapezoid