In this post, we summarize the previous three articles about domain and range. In the first part of the series, we focused on the graphical meaning of domain and range. We have learned that the domain of a function can be interpreted as the projection of its graph to the x-axis. Similarly, the range of the function is the projection of its graph to the y-axis.
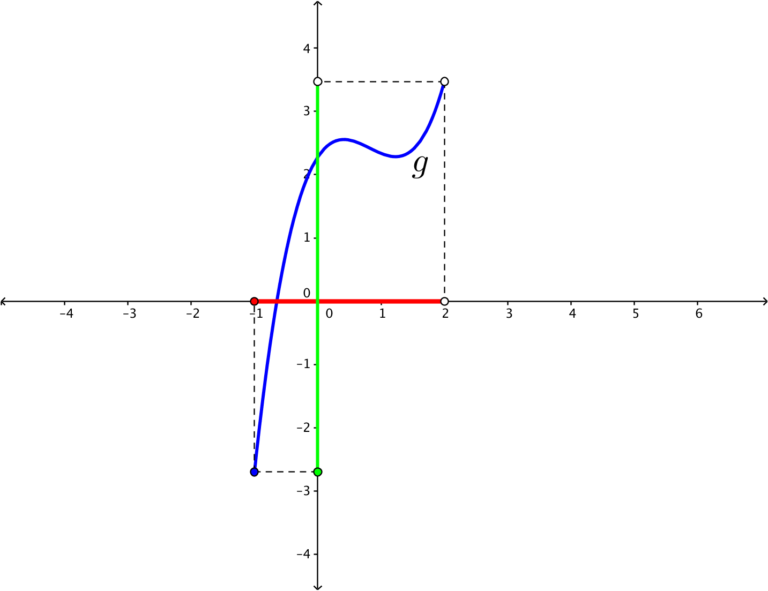
Graphical meaning of domain (red) and range (green)
In the second part of the series, we learned to analyze equations of functions to determine their domain and range. We learned the restrictions in the domain and range of functions are affected by the following: squares in the expressions, square root signs, absolute value signs, and being in the denominator. In exploring these we concluded the following:
- Expressions under the square root sign result to a positive real number or 0. This means that we have to set the inequality such that the expression is greater than or equal to 0, and then find the permissible values of x.
- Expressions containing squares result to a positive real number or 0. This affects the range of the function.
- Expressions inside the absolute value sign result to a positive number of 0. This also affects the range of the function.
- Expressions in the denominator of fractions cannot be 0 because it will make the function undefined. So, we need to find the value of x that makes the denominator by 0. To do this, we equate the expression in the denominator to 0 and find the value of x. The values of x are the restrictions in the domain.
In the third part of the series, we examined functions that have more complicated equations than those in the second part of the series.
Before I end this series, there is one more concept about domain that I want you to remember. That is, the domain of all polynomial functions is the set of real numbers. That’s why the domain of linear functions and quadratic functions in Part 1 and Part 2 is the set of real numbers.