Understanding Domain and Range Part 2
In the previous post, we have learned the graphical representation of domain and range. The domain of the function is the shadow or projection of the graph of
to the x-axis (see the red segment in the figure below). The range of
is the projection of the graph of
to the y-axis (see the green segment in the figure below). In this post, we are going to learn how to analyze equations of functions and determine their domain and range without graphing.
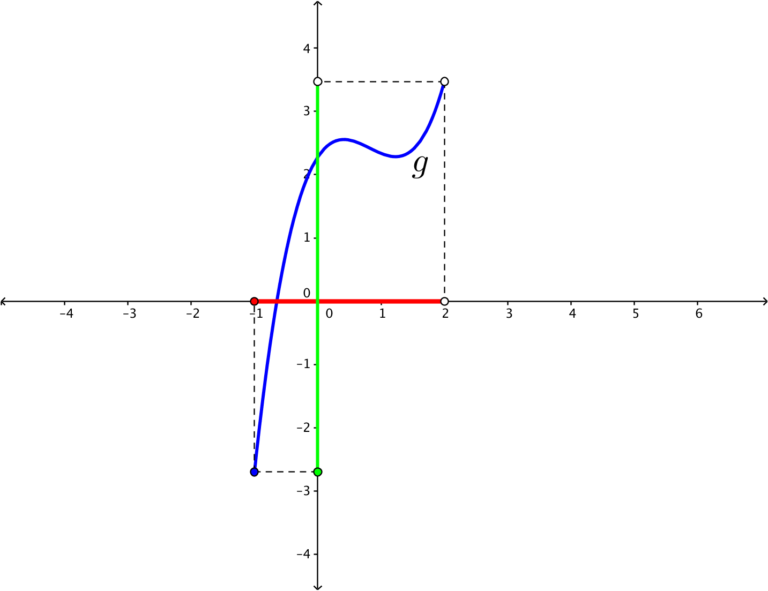
If a graph of a function is projected to the x-axis, the projection is the set of x-coordinates of the graph. A single point on the projection means a point on the graph exists. The existence of a point implies that
exists. This means that the function is defined at
. In effect, the domain of a function is the set of x-coordinates that makes the function defined. In what follows, we learn some examples to illustrate this concept.
Example 1: Find the domain and range of .
Explanation
As we can see from the equation, we can substitute any real number to and any of these values makes the function defined. Therefore, the domain of the function
is the set of real numbers. The range of the function has also no restriction. We can think of any real number
, and we can always find the corresponding
by subtracting 1 from it. Therefore, the range of
is the set of real numbers.
Example 2: Find the domain and range of .
Explanation
Just like in Example 1, we can substitute any real number to and any of them makes
defined (Can you see why?). So, the domain of
is the set of real numbers.
Now let’s think about the range. The range are the values of . Notice that if we square a positive real number, the result is a positive real number. If we square a negative real number, then the result is also a positive real number. If we square 0, the result is 0. Therefore, the only possible results that we can get if we square a real number are 0 and positive real numbers. Therefore, the range of
is the set of real numbers greater than, or equal to 0. In interval notation, the range of
is
.
Example 3: Find the domain and range of
Recall that means the absolute value of
. As we can see, we can substitute any real number to
, and
is always defined. So, the domain of
is the set of real numbers.
As for the range, if is a negative real number, then
is a positive real number. If
is
,
is also
. If
is a positive real number, then
is a positive real number. Since all values of
is either 0 or positive real numbers, the range of
, is the set of real numbers greater than or equal to 0. In interval notation, the range of
is
.
Example 4: Find the domain and range of
Explanation
We know that we cannot find a real number that is a square root of negative numbers. This means that we cannot substitute a negative number for . In effect, we limit the
values of
to 0 and positive real numbers. Therefore, the domain of
is the set of real numbers greater than or equal to 0. In interval notation, the domain of
is
.
Since we are only allowed to substitute and positive real numbers to
, then, it follows that
will also result to 0 or a positive real number. Therefore, the range of
is the set of real numbers greater than or equal to 0. In interval notation, the range of
is
.
Example 5: Find the domain of
Explanation
We know that we cannot have a zero denominator because it will make the fraction undefined, so cannot equal to 0. But aside from 0, we can substitute any value to
, so, the domain of
is the set of real numbers except 0. In interval notation, the domain of
is
.
For the range, examine the equation . We can get
that are small by substituting large values to
. We can also get
that are large by substituting small values to
. We can also choose an
that will make
negative. But we cannot get a value of
, because the only way to do this is for the numerator of the expression to be 0. But our expression is
, so
cannot be 0. Therefore, the range of
is the set of real numbers except 0. In interval notation, the range of
is
is
.
In the next post, we will have more examples on how to determine the domain and range of a function.