Real Numbers: A Summary
For the past two years, we have talked a lot about real numbers. We have talked about integers and its operations (addition, subtraction, multiplication, and division), we have discussed about rational and irrational numbers, and we have talked about their properties, structure, and wonders. In this post, we are going to summarize what we have learned about them.
Figure 1 - The Number Line
The set of real numbers is the collection of all rational and irrational numbers. By convention, real numbers are represented by a line infinitely long where the positive real numbers are situated at the right hand side of 0, while the negative are at the left hand side. It is also important to note that for each point on the number line, there exists a corresponding real number equivalent to it, and for each real number, there is a corresponding point on the line that represents it.
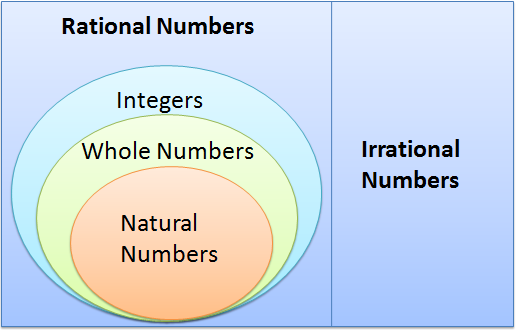
The structure of the real number system is shown in the second figure. It is divided into two sets – the set of rational numbers and the set of irrational numbers. The rational numbers has several subsets as shown: the set of natural numbers (1, 2, 3,…), set of whole numbers (0, 1, 2, 3,…), and set of integers (0, 1, -1, 2, -2, 3, -3,… ). Needless to say, we can see from the figure that the set of natural numbers is a subset of the set of whole numbers, and that the set of whole numbers is a subset of the set of integers.
We have also learned the different properties of real numbers. We have discussed that real numbers are
(1) commutative under addition and multiplication; that is, for all real numbers a and b, a + b = b + a and ab = ba
(2) associative under addition and multiplication; that is, for all real numbers a, b, and c, (a+b) + c = a + (b+c).
(3) distributive over addition. That is, for all real numbers a, b, and c, a(b + c) = ab + ac.
Now we learn other properties that we have not discussed before. We discuss the existence of identity and inverses of addition and multiplication.
(4) identity for addition and multiplication. For addition, for all real numbers a there exists a number 0 such that a + 0 = a = 0 + a; for multiplication, for all real numbers a, there exists a number 1 such that a(1) = a = (1)(a)
(5) inverses. For all real numbers a, there exists an additive inverse –a such that a + –a = 0 = –a + a; for all real numbers a, there exists a multiplicative inverse 1/a such that a(1/a) = 1 = (1/a)(a)
We should also note the discussion on the closure of real numbers. That is if we add, subtract, or multiply a real number to/by a real number, the result is still a real number. The division of real numbers is not closed since we cannot divide any real number by 0.