Operations on Integers – Subtraction
We have discussed about addition of integers and its representation as chips. Recall in our previous discussion that a single positive chip added up to a single negative chip is equal to 0. The addition below as we have discussed will give us a notion of how to add signed numbers.
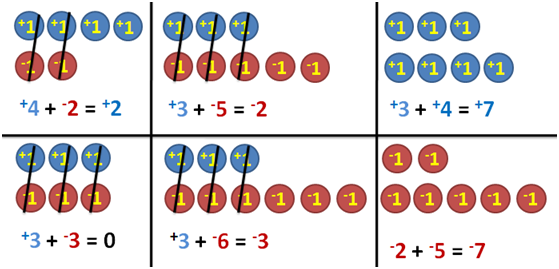
Now let us discuss on how use signed chips can be used as a strategy to subtract integers. Let us represent the following using chips.
- +7 – +4
- +3 – +5
- +5 – (–3)
- –3 – (–4)
- -5 – +2
Before discussing subtraction of integers using signed chips, let us recall some concepts. First, we know that any number added to 0 is equal to that number. That is, if n + 0 = n for any number n. Second, if we add the same number of positive and negative chips to n, then we are just adding 0; therefore, it does not change the value of n.
We will also agree on the following. First, we can think of subtraction as “taking away,” and second, when we say positive chip, we mean+1 chip, unless stated otherwise. This means that we when we say 3 positive chips, we mean three pieces of +1 chips.
Case 1: +7 – +3
The solution for case 1 is very obvious. +7 – +4 is equal to +3. But if we represent it using the chips, we have 7 positive chips and we want to take away 3 positive chips. So, the answer is 3 chips. Again, +7 – +3 = +4.
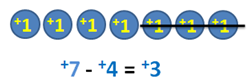
Case 2: +3 – +5
In the second problem, we have three positive chips, and we want to take away 5 positive chips. We have a slight problem; we don’t have enough chips to take away!
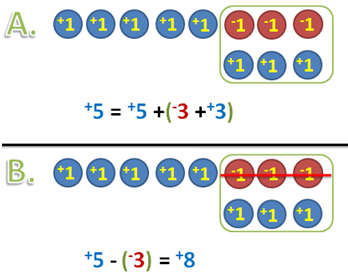
Hmm…. but we can use the second concept that we have recalled above. . In A (in the second figure), we need 5 chips so we can add 2 more positive chips, but that will change our original number of chips to +5. To remedy this problem, we add another two negative chips to cancel out the +2 that we have added. Note that we added +2 and added –2, which means that we added 0. In B, we represented +3 with +5 and –2 chips. Now, we can take away +5 and we are left with -2. Therefore, +3 – +5 = –2.

Case 3: +5 – (–3)
In the third case, we have 5 positive chips, and we want to take away 3 negative chips. Again we don’t have negative chips. Just like in case 2, we add -3 and +3 chips which mean that just added 0. Therefore +5 – (–3) = +8
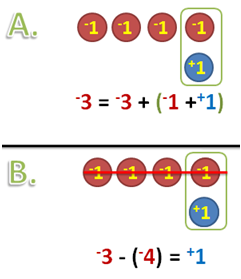
Case 4: –3 – (–4)
In A, we have 3 negative chips and we take away 4 negative chips, so we add 1 negative chip and 1 positive chip which is equivalent to adding 0. In B, we already have four negative chips and 1 positive chip; we take away four negative chips and we are left with 1 positive chip. Therefore, –3 – (–4) = +1
Case 5: –5 – +2
In A, we have 5 negative chips and we want to take away 2 negative chips. So we add 0 by adding 2 positive chips and 2 negative chips. In B, we have 7 negative chips and 2 positive chips. We take away +2. We are left with 7 negative chips. Therefore, –5 – +2 = –7

The five cases above also review us of what we have learned in addition of integers. In case 2, we have +3 = +5 + (–2); in case 3, we have +8 + (–3) = +5; in case 4, we have –3 = –4 + +1; and in case 5, we have –5 = –7 + +2.