Operations on Integers – Subtraction
We have discussed about addition of integers and its representation as chips. Recall in our previous discussion that a single positive chip added up to a single negative chip is equal to 0. The addition below as we have discussed will give us a notion of how to add signed numbers.
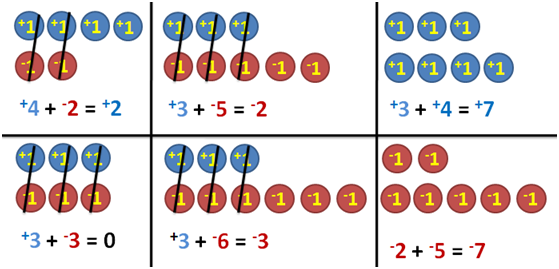
Now let us discuss on how use signed chips can be used as a strategy to subtract integers. Let us represent the following using chips. » Read more