Military drills and the closure property of real numbers
In military drills, we are familiar with the commands that let the soldiers face or turn to certain directions. Left face (sometimes called left turn), right face, and about face are probably the most common commands used. If we are facing north, a left face would mean turning left 90 degrees, which means facing west. In the following discussion, we will agree that our starting position is facing north. We will call this position, the standard position.
Let us represent the turns with letters:A for about face, R for right face, and L for left face. Notice that whatever combination of turns we do, L, R or A, the result is confined to the four directions. An R followed by an A is equivalent to an L (facing west) with respect to the standard position. Likewise an L followed by another L is equivalent to A.We will to denote our starting position P as reference; it is not turn command, so if the soldier is not facing north (see second figure), a P will just mean that the soldiers remain in their current position.
If we let F be the set of all possible turns as have agreen, then F = {P, A, L, R} In fact, if we are going to represent turning as *, we can construct a table such as the one shown below.

Notice that the result of the operation between two elements in the set F is also in F. For instance, A*A = P, L*A = R, P*L = L and so on. This characteristic of F is called the closure property. We say that the set F is closed under the operation *. To give you a better understanding, let us discuss a few more concrete examples.
Example 1
Let G = {1, 0, -1}. As shown in the table below, if we multiply any elements of G, the product is also in G (the products are either 1,0 or -1). Therefore, we can say that G is closed under multiplication.
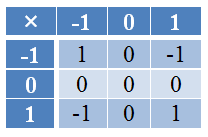
Obviously, G is not closed under addition since 1 + 1 = 2 and 2 is not in G. It is not also closed under division since 1/0 is undefined.
Example 2
The set of natural numbers {1,2,3, …} is closed under addition and multiplication, because if you add/multiply any natural number by any natural number, the result is also a natural number.
The set of natural numbers is not closed under subtraction since 1 – 3 = -2 and -2 is not a natural number.
The set of natural numbers is not closed under division since ½ = 0.5 is not a natural number.
Example 3
The set of irrational numbers is not closed under addition because +
and 0 is a rational number.
Most number systems are closed in certain operations, but as you have observed, most of them are not closed under the certain operations. The binary, octal, and hexadecimal numbers are closed under addition, subtraction, and multiplication. (Are they closed under division?).
The set of real numbers are closed under addition, subtraction, multiplication, but not closed under division.
Exercise
Explain the closure property of the following numbers under four fundamental operations unless specified:
- set of rational numbers
- set of negative integers
- set of irrational numbers under multiplication and division
- set of non-negative integers
***
Photo Credit: The US Army
Related Articles
