The Commutativity of Real Numbers
In the previous discussion, we have shown that addition of two integers a and b is commutative by considering a and b as lengths of two segments. Joining the two segments is the same as adding two integers. We have observed that a + b equals b + a.
We have also shown that multiplication of two integers a and b is commutative by considering a and b as side lengths of a rectangle. Getting the area of a rectangle with side lengths a and b is the same as multiplying a and b. We have observed that ab equals ba. However, we argued about commutativity that any segment does not change its length and the movement of rectangles does not change its area. This reasoning is only limited to positive integers because we cannot represent negative integers as length or area. To explore further, we use the addition and multiplication tables to see if the addition and multiplication of integers are both commutative.
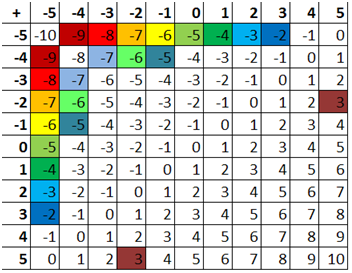
Consider the addition table above. As indicated by the cells with similar colors, it is not difficult to see that the table is symmetric with respect to the diagonal cells from -10 down to 10 as line of symmetry. Take for example -6 in the yellow cells: they shows that -1 + -5 = -5 + -1.
Also, notice that the cells in similar colors shows that a + b = b + a, whether they are positive or negative. If we extend the table, it is clear that it will always be symmetric. Therefore, looking at the pattern, we can conclude that the addition of integers is commutative; that is, for all integers a and b, a + b = b + a.
The commutativity property is not true for subtraction. We just need one counterexample to show that it is not true. One example is 2 – 5 does not equal to 5 – 2.
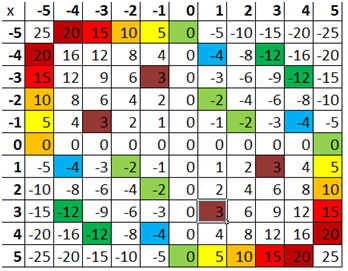
Looking at the multiplication table below, we can also see by looking at the colored cells that the table is also symmetric; in fact, symmetric with respect to both diagonals. Therefore, multiplication of integers is also commutative.
Of course, division of integers is not commutative since 1/2 is not equal to 2/1.
The commutative property of addition and multiplication is not only true for integers, but is also true for all real numbers. We can see this by constructing a similar table as the two tables shown above, only that the numbers are decimals.